题目内容
9.已知曲线C1的参数方程为$\left\{\begin{array}{l}{x=cost}\\{y=1+sint}\end{array}\right.$(t为参数),以坐标原点为极点,x轴正半轴为极轴,曲线C2的极坐标方程为ρcosθ=-$\frac{\sqrt{3}}{2}$.(1)把曲线C1的参数方程化为极坐标方程;
(2)求曲线C1与曲线C2的交点的极坐标.
分析 (1)先把C1的参数方程化为普通方程,再化为极坐标方程;
(2)求出C2的普通方程,与C1的普通方程联立解出交点的直角坐标,转化为极坐标.
解答 解:(1)曲线C1的普通方程为x2+(y-1)2=1,即x2+y2-2y=0,
∴曲线C1的极坐标方程为ρ2-2ρsinθ=0,即ρ=2sinθ.
(2)曲线C2的普通方程为x=-$\frac{\sqrt{3}}{2}$.
把x=-$\frac{\sqrt{3}}{2}$代入x2+y2-2y=0得y=$\frac{1}{2}$或y=$\frac{3}{2}$.
∴曲线C1与曲线C2的交点的直角坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
∴曲线C1与曲线C2的交点的极坐标为(1,$\frac{5π}{6}$),($\sqrt{3}$,$\frac{2π}{3}$).
点评 本题考查了极坐标方程,参数方程与普通方程的转化,属于中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
4.在△ABC中,A=60°,AC=2,BC=$\sqrt{7}$,则AB等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{1+\sqrt{13}}{2}$ |
18.已知U=R,函数y=log2(2-x)的定义域为M,N={x|x2-2x<0},则下列结论正确的是( )
| A. | M∩(∁UN)=∅ | B. | M∩N=N | C. | M∪N=U | D. | M⊆(∁UN) |
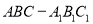 中,平面
中,平面 侧面
侧面 ,且
,且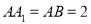 .
.
 ;
;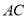 与平面
与平面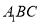 所成角的正弦值为
所成角的正弦值为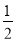 ,求锐二面角
,求锐二面角 的大小.
的大小. (
( ),其中
),其中 为虚数单位,则
为虚数单位,则 ( )
( )