题目内容
17.在极坐标系中,曲线ρ=sinθ+2与ρsinθ=2的公共点到极点的距离为1+$\sqrt{3}$.分析 联立方程组 消去sinθ求解即可.
解答 解:ρ=sinθ+2与ρsinθ=2消去sinθ,可得ρ(ρ-2)=2,由于ρ>0,解得ρ=1+$\sqrt{3}$.
故答案为:$1+\sqrt{3}$.
点评 本题考查极坐标方程的应用,利用ρ的几何意义是解题的关键.

练习册系列答案
相关题目
2.若函数f(x)=3-sinωx-$\sqrt{3}$cosωx(x∈R)的图象向右平移$\frac{4π}{3}$个单位后与原图象重合,则正数ω的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{1}{3}$ |
6.设a=$\frac{1}{2}$cos6°-$\frac{\sqrt{3}}{2}$sin6°,b=sin26°,c=$\sqrt{\frac{1-cos50°}{2}}$,则有( )
| A. | a>b>c | B. | a<b<c | C. | a<c<b | D. | b<c<a |
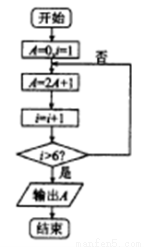
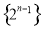 前5项的和 B.计算数列
前5项的和 B.计算数列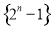 前5项的和
前5项的和 
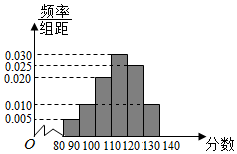 2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[120,130),[130,140)后得到如图所示的频率分布直方图.
2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[120,130),[130,140)后得到如图所示的频率分布直方图.