��Ŀ����
1����֪ԲC��$\left\{\begin{array}{l}{x=1+cos��}\\{y=sin��}\end{array}\right.$����Ϊ��������ֱ��l��$\left\{\begin{array}{l}{x=2++tcos��}\\{y=\sqrt{3}+tsin��}\end{array}\right.$������tΪ��������Ϊ��б�ǣ���1������=$\frac{��}{3}$ʱ����Բ�ϵĵ㵽ֱ��l�������Сֵ��
��2����ֱ��l��ԲC�й�����ʱ�������ȡֵ��Χ��
���� ��1�����Բ��ֱ�ߵ���ͨ���̣�����Բ�ĵ�ֱ�ߵľ����ж�ֱ����Բ��λ�ù�ϵ���ó�������Сֵ��
��2�����Բ���㣨2��$\sqrt{3}$�������ߵ���б�ǣ������ֵ�����������ߵ���б��֮�䣮
��� �⣺��1��Բ�ı�����Ϊ��x-1��2+y2=1��
��$��=\frac{��}{3}$ʱ��ֱ��l��б��Ϊ$\sqrt{3}$���ҹ��㣨2��$\sqrt{3}$����
��ֱ��l����ͨ����Ϊ3x-$\sqrt{3}$y-3=0��
��Բ�ĵ�ֱ��l�ľ���d=0��
��ֱ��l��Բ�ཻ��
��Բ�ϵĵ㵽ֱ��l�������СֵΪ0��
��2������=$\frac{��}{2}$ʱ��ֱ��l�ķ���Ϊx=2����Ȼ��Բ���У�
��Բ���㣨2��$\sqrt{3}$�������߷���Ϊy-$\sqrt{3}$=k��x-2������kx-y-2k+$\sqrt{3}$=0��
��Բ�ĵ����ߵľ���$\frac{|k-2k+\sqrt{3}|}{\sqrt{{k}^{2}+1}}$=1��
���k=$\frac{\sqrt{3}}{3}$��
�����ߵ���б��Ϊ$\frac{��}{6}$��
��ֱ��l��Բ�й����㣬
��$\frac{��}{6}�ܦ���\frac{��}{2}$��
���� ���⿼���˲�����������ͨ���̵�ת����ֱ����Բ��λ�ù�ϵ�������е��⣮

��ϰ��ϵ�д�
�����Ŀ
16������$\frac{i^3}{2i-1}$��iΪ������λ���Ĺ�����ǣ�������
| A�� | $-\frac{2}{5}+\frac{1}{5}i$ | B�� | $\frac{2}{3}+\frac{1}{3}i$ | C�� | $\frac{2}{3}-\frac{1}{3}i$ | D�� | $-\frac{2}{5}-\frac{1}{5}i$ |
6����a=$\frac{1}{2}$cos6��-$\frac{\sqrt{3}}{2}$sin6�㣬b=sin26�㣬c=$\sqrt{\frac{1-cos50��}{2}}$�����У�������
| A�� | a��b��c | B�� | a��b��c | C�� | a��c��b | D�� | b��c��a |
13�����ABC���ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c����b2=a2+c2+2accosB�����B=��������
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{��}{2}$ | D�� | $\frac{2��}{3}$ |

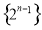 ǰ5��ĺ� B����������
ǰ5��ĺ� B����������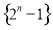 ǰ5��ĺ�
ǰ5��ĺ� 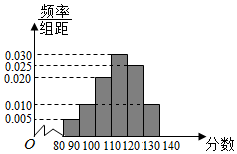 2015����ѧ��ij�н����ֶ�ijУ�����Ŀ���ѧ���н�ѧ���У��Ӹ�У�Ŀ����������ȡ40��ѧ������ѧ�ɼ�����ͳ�ƣ������ǵijɼ��ֳ�����[80��90����[90��100����[100��110����[120��130����[130��140����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
2015����ѧ��ij�н����ֶ�ijУ�����Ŀ���ѧ���н�ѧ���У��Ӹ�У�Ŀ����������ȡ40��ѧ������ѧ�ɼ�����ͳ�ƣ������ǵijɼ��ֳ�����[80��90����[90��100����[100��110����[120��130����[130��140����õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��