题目内容
4.在△ABC中,A=60°,AC=2,BC=$\sqrt{7}$,则AB等于( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{1+\sqrt{13}}{2}$ |
分析 由AC,BC以及cosA的值,利用余弦定理即可求出AB的值.
解答 解:∵在△ABC中,A=60°,AC=2,BC=$\sqrt{7}$,
∴由余弦定理得:BC2=AC2+AB2-2AC•ABcosA=4+AB2-2×2×AB×$\frac{1}{2}$=7,
则解得:AB=-1或3(舍去).
故选:C.
点评 此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键,属于基础题.

练习册系列答案
相关题目
某同学寒假期间对其30位亲属的饮食习惯进行了一次调查,列出了如下 列联表:
列联表:
偏爱蔬菜 | 偏爱肉类 | 合计 | |
50岁以下 | 4 | 8 | 12 |
50岁以上 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
则可以说其亲属的饮食习惯与年龄有关的把握为( )
A.90% B.95% C.99% D.99.9%
附:参考公式和临界值表

| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
16.复数$\frac{i^3}{2i-1}$(i为虚数单位)的共轭复数是( )
| A. | $-\frac{2}{5}+\frac{1}{5}i$ | B. | $\frac{2}{3}+\frac{1}{3}i$ | C. | $\frac{2}{3}-\frac{1}{3}i$ | D. | $-\frac{2}{5}-\frac{1}{5}i$ |
13.设△ABC的内角A,B,C所对的边分别为a,b,c,且b2=a2+c2+2accosB,则∠B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
13.已知等比数列{an}满足a1=3,a1+a3+a5=21,则a3+a7=( )
| A. | 18 | B. | 24 | C. | 30 | D. | 42 |
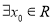 使不等式
使不等式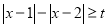 成立.
成立.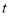 的集合
的集合 ;
;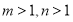 ,对
,对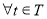 ,不等式
,不等式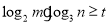 恒成立,求
恒成立,求 的最小值.
的最小值.

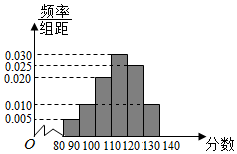 2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[120,130),[130,140)后得到如图所示的频率分布直方图.
2015年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取40名学生的数学成绩进行统计,将他们的成绩分成六段[80,90),[90,100),[100,110),[120,130),[130,140)后得到如图所示的频率分布直方图.