题目内容
13.化简:(1)$\frac{sin(2π+α)•cos(7π-α)}{cos(-α)}$;
(2)已知cosα=-$\frac{3}{5}$,α∈($\frac{π}{2}$,π),求tan(5π-α)的值.
分析 (1)直接利用诱导公式化简得答案;
(2)由已知求得sinα,再由诱导公式及同角三角函数的基本关系式求得答案.
解答 解:(1)$\frac{sin(2π+α)•cos(7π-α)}{cos(-α)}$=$\frac{sinα•cos(π-α)}{cosα}$=$\frac{sinα•(-cosα)}{cosα}$=-sinα;
(2)由cosα=-$\frac{3}{5}$,α∈($\frac{π}{2}$,π),得$sinα=\sqrt{1-co{s}^{2}α}=\sqrt{1-(-\frac{3}{5})^{2}}=\frac{4}{5}$,
则tan(5π-α)=-tanα=-$\frac{sinα}{cosα}=-\frac{\frac{4}{5}}{-\frac{3}{5}}=\frac{4}{3}$.
点评 本题考查三角函数的化简求值,考查了诱导公式及同角三角函数基本关系式的应用,是基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.设数列{an}是等差数列,且a4=-4,a9=4,Sn是数列{an}的前n项和,则( )
| A. | S5<S6 | B. | S5=S6 | C. | S7=S5 | D. | S7=S6. |
4.如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖块数为( )
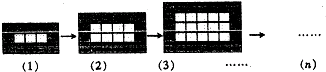

| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
18.3名同学分别报名参加学校的足球队,篮球队,乒乓球队,排球队,每人限报其中的一个运动队,不同报法的种数是( )
| A. | 34 | B. | 43 | C. | 24 | D. | 12 |
5.设正数数列{an}的前n项和为bn,数列{bn}的前n项之积为cn,且bn+cn=1,则数列{$\sqrt{\frac{1}{{a}_{n}}}$}的前n项和Sn中大于2016的最小项为第63项.
2.设数列{an}是公差不为零的等差数列,且a1,a3,a7构成等比数列,则公比q为( )
| A. | $\sqrt{2}$ | B. | 4 | C. | 2 | D. | $\frac{1}{2}$ |