题目内容
9.某种产品的广告费支出x与销售额y(单位:万元)之间有如表对应数据:| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
已知b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
分析 (1)首先求出x,y的平均数,利用最小二乘法做出线性回归方程的系数,根据样本中心点满足线性回归方程,代入已知数据求出a的值,写出线性回归方程.
(2)分别求出在已有的五组数据中任意抽取两组的情况总数,及至少有一组数据其预测值与实际值之差的绝对值不超过5的情况数,代入古典概型概率计算公式,可得答案.
解答 解:(1)由题意得$\overline{x}=\frac{2+4+5+6+8}{5}=5$,$\overline{y}=\frac{30+40+50+60+70}{5}=50$,$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n•\bar x•\bar y}}{{\sum_{i=1}^n{x_i^2}-n•{{\bar x}^2}}}=\frac{60+160+300+300+560-5×5×50}{4+16+25+36+64-5×25}=\frac{130}{20}=\frac{13}{2}$,
$a=\bar y-b\overline{x}=25-\frac{13}{2}×5=\frac{35}{2}$,
所求回归直线方程为$\hat y=\frac{13}{2}x+\frac{35}{2}$;
(2)基本事件:(30,40),(30,60),(30,50),(30,70),
(40,60),(40,50),(40,70),(60,50),(60,70),(50,70)共10个
两组数据其预测值与实际值之差的绝对值都超过5:(60,50)
所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为${P}=1-\frac{C_2^2}{C_5^2}=1-\frac{1}{10}=\frac{9}{10}$.
点评 本题考查回归分析的初步应用,考查求线性回归方程,考查预报y的值,是一个综合题目,解此类题,关键是理解线性回归分析意义.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案①10件产品中有2件次品,从中任选3件,取到次品的件数X;
②一位射击手对目标进行射击,击中目标得1分,未击中目标得0分,用X表示该射击手在一次射击中的得分;
③刘翔在一次110米跨栏比赛中的成绩X;
④在体育彩票的抽奖中,一次摇号产生的号码数X.
其中X是离散型随机变量的是( )
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ③④ |
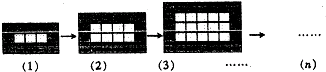
| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
| A. | 34 | B. | 43 | C. | 24 | D. | 12 |
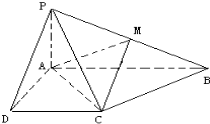 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.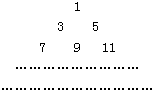 把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表:
把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如图三角形数表: