Question

若不等式x²-log_mx＞0在（

1

2

，1）范围内恒成立，则实数m的取值范围是（　　）

• A、[

  1

  16

  ，1)
• B、(0，

  1

  16

  ]∪（1，+∞）
• C、(0，

  1

  16

  )∪（1，+∞）
• D、[

  1

  16

  ，1)∪（1，+∞）

Answer 1

考点：其他不等式的解法

专题：不等式的解法及应用

分析：问题转化为x∈（

1

2

，1）时，函数f（x）=x²的图象恒在g（x）=log_mx的图象的上方，数形结合可得．

解答： 解：不等式x²-log_mx＞0，在（

1

2

，1）范围内恒成立，
可转化为x²＞log_mx，在（

1

2

，1）范围内恒成立，
即x∈（

1

2

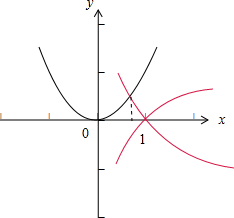
，1）时，函数f（x）=x²的图象恒在g（x）=log_mx的图象的上方．
由图象可知当m＞1时恒成立，
当0＜m＜1，若x=

1

2

时，两图象相交，即(

1

2

)2=log_m

1

2

，解得m=

1

16

，
∴m范围为：（0，

1

16

]
综合可得实数m的取值范围为：（0，

1

16

]∪（1，+∞）
故选：B

点评：本题考查不等式的恒成立问题，数形结合是解决问题的关键，属基础题．