题目内容
12.画出计算1+2+$\frac{1}{2}$+3+$\frac{1}{3}$+…+2008+$\frac{1}{2008}$的算法框图,并编写出与框图对应的算法语句.分析 这是一个累加求和问题,可设计一个计数变量,一个累加变量,用循环结构实现这一算法,利用框图,即可写出对应的算法语句.
解答  解:程序框图:(8分)
解:程序框图:(8分)
程序:
i═2
s=1
DO
s=s+i+$\frac{1}{i}$
i=i+1
LOOP UNTIL i>2008
PRINT S
END (l2分)
点评 本题主要考查设计程序框图解决实际问题.在一些算法中,也经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构.循环结构要在某个条件下终止循环,这就需要条件分支结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果,计数变量和累加变量一般是同步执行的,累加一次,计数一次,属于基础题.

练习册系列答案
相关题目
2.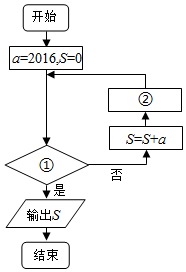 如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
 如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )
如图表示的是求首项为2016,公差为-3的等差数列{an}前n项和的最大值的程序框图,则①和②处可填写( )| A. | ①a<0?,②a=a-3 | B. | ①a<0?,②a=a+3 | C. | ①a>0?,②a=a-3 | D. | ①a>0?,②a=a+3 |
17.设集合A={4,5,6,9},B={3,4,6,8,9},全集U=A∪B,则集合∁U(A∩B)的元素个数共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
4.已知直线l与直线2x-y+4=0关于x=1对称,则直线l的方程是( )
| A. | 2x+y-8=0 | B. | 3x-2y+1=0 | C. | x+2y-5=0 | D. | 3x+2y-7=0 |
1.若直线l与直线y=2,x=4分别交于点P,Q,且线段PQ的中点坐标为(1,-1),则直线l的斜率为( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
2.将4个球随机放入3个空盒,则所有球都在两个盒中,但不是全在一个盒子里的概率为( )
| A. | $\frac{7}{27}$ | B. | $\frac{2}{3}$ | C. | $\frac{14}{27}$ | D. | $\frac{14}{81}$ |