题目内容
1．若直线l与直线y=2，x=4分别交于点P，Q，且线段PQ的中点坐标为（1，-1），则直线l的斜率为（ ）| A． | 1 | B． | -1 | C． | -3 | D． | 3 |
分析 利用中点坐标公式可得P，Q，再利用斜率的计算公式即可得出．
解答 解：设P（x，2），Q（4，y）．
∵线段PQ的中点坐标为（1，-1），
∴$\left\{\begin{array}{l}{\frac{x+4}{2}=1}\\{\frac{2+y}{2}=-1}\end{array}\right.$，解得x=-2，y=-4．
∴P（-2，2），Q（4，-4）
∴直线l的斜率=$\frac{2+4}{-2-4}$=-1．
故选：B．
点评 本题考查了中点坐标公式、斜率的计算公式，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
11．
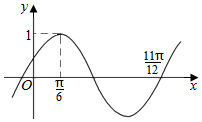函数$f（x）=Asin（ωx+φ）\;（A＞0\;，\;ω＞0\;，\;|φ|＜\frac{π}{2}）$的部分图象如图所示，则将y=f（x）的图象向右平移$\frac{π}{6}$个单位后，得到的函数图象的解析式为（ ）
函数$f（x）=Asin（ωx+φ）\;（A＞0\;，\;ω＞0\;，\;|φ|＜\frac{π}{2}）$的部分图象如图所示，则将y=f（x）的图象向右平移$\frac{π}{6}$个单位后，得到的函数图象的解析式为（ ）| A． | y=sin2x | B． | $y=sin（2x+\frac{2π}{3}）$ | C． | $y=sin（2x-\frac{π}{6}）$ | D． | y=cos2x |
9．
如图所示的小方格是边长为1的正方形，在复平面内，若复数z1，z2对应的向量分别是$\overrightarrow{{O}{A}}$，$\overrightarrow{{O}{B}}$，则$\overrightarrow{AB}$所对应的复数为（ ）
如图所示的小方格是边长为1的正方形，在复平面内，若复数z1，z2对应的向量分别是$\overrightarrow{{O}{A}}$，$\overrightarrow{{O}{B}}$，则$\overrightarrow{AB}$所对应的复数为（ ）| A． | -3i | B． | 2i | C． | 1-2i | D． | 1+2i |