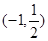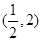题目内容
已知函数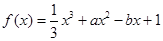 (
( 为实数)有极值,且在
为实数)有极值,且在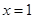 处的切线与直线
处的切线与直线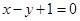 平行.
平行.
(1)求实数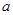 的取值范围;
的取值范围;
(2)是否存在实数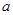 ,使得函数
,使得函数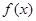 的极小值为
的极小值为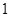 ,若存在,求出实数
,若存在,求出实数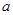 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设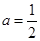 ,
,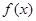 的导数为
的导数为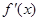 ,令
,令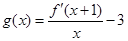
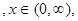
求证: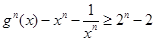
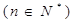
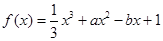 (
(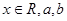 为实数)有极值,且在
为实数)有极值,且在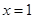 处的切线与直线
处的切线与直线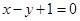 平行.
平行.(1)求实数
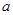 的取值范围;
的取值范围;(2)是否存在实数
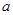 ,使得函数
,使得函数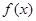 的极小值为
的极小值为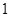 ,若存在,求出实数
,若存在,求出实数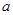 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)设
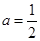 ,
,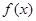 的导数为
的导数为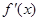 ,令
,令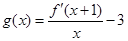
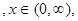
求证:
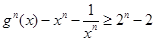
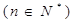
(1) 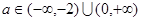 (2)存在
(2)存在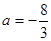 . (3)略
. (3)略
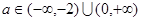 (2)存在
(2)存在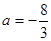 . (3)略
. (3)略(1)根据极值的信息,则选用导数法,先求f'(x),再由f(x)有极值,可有=a2-4b>0,又由在x=-1处的切线与直线x-y+1=0平行,可得f'(-1)=1-a+b=1从而求解
(2)先假存在,则根据条件,则有关于a的不等式,进而得到范围。
(3)构造函数利用导数的思想求解函数的最值得到证明
(1)∵
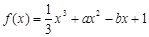 ,∴
,∴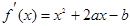 ,
,由题意∴
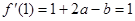 ,
,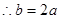 ① ……2分
① ……2分∵
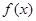 有极值,∴方程
有极值,∴方程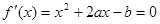 有两个不等实根.
有两个不等实根.∴
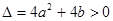 、 ∴
、 ∴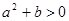 . ②
. ②由①、②可得,
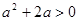 . ∴
. ∴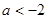 或
或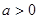 .
.故实数
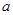 的取值范围是
的取值范围是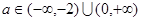 …2分
…2分(2)存在
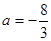 .……………1分
.……………1分 由(1)令
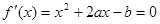 ,
,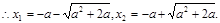

∴
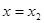 时,
时,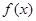 取极小值,则
取极小值,则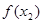 =
=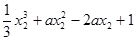
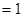 ,
,∴
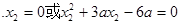 ……………………………………………………2分
……………………………………………………2分若
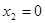 ,即
,即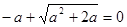 则
则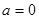 (舍).……………………1分
(舍).……………………1分若
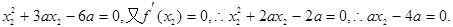
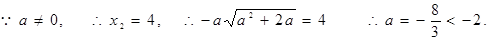
∴存在实数
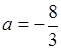 ,使得函数
,使得函数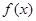 的极小值为1 ………1分
的极小值为1 ………1分(3)∵
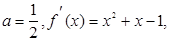
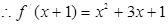 ,
, 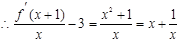
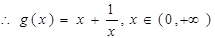 …….l分
…….l分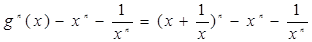
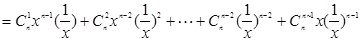
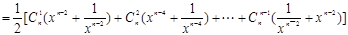
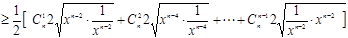
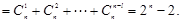
∴其中等号成立的条件为
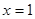 ………………3分
………………3分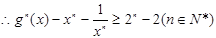

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
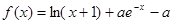 ,
,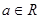 .
.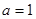 时,证明
时,证明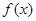 在
在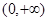 是增函数;
是增函数;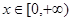 ,
,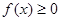 ,求
,求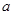 的取值范围.
的取值范围.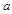 为实数,
为实数,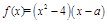 ,
,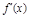 为
为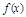 的导函数.
的导函数.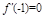 ,求
,求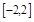 上的最大值和最小值;
上的最大值和最小值;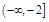 和
和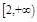 上均单调递增,求
上均单调递增,求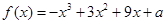 (
(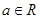 )
) 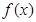 的极大值和极小值;
的极大值和极小值;
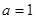 时, 求函数
时, 求函数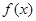 的单调增区间;
的单调增区间;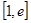 上的最小值;
上的最小值;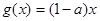 ,若存在
,若存在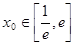 ,使得
,使得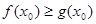 成立,求实数
成立,求实数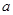 的取值范围.
的取值范围.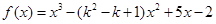 ,
,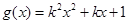 ,其中
,其中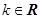 .
. 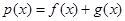 ,若
,若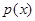 在区间
在区间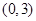 是单调函数,求
是单调函数,求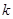 的取值范围;
的取值范围;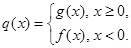 ,是否存在
,是否存在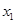 ,存在惟一的非零实数
,存在惟一的非零实数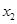 (
(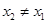 ),使得
),使得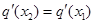 成立?若存在,求
成立?若存在,求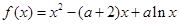 ,其中
,其中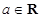 .
.  的图象在点
的图象在点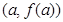 处的切线与直线
处的切线与直线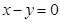 平行,求实数
平行,求实数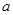 的值;
的值;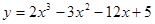 在[0,3]上的最大值,最小值分别是 ( )
在[0,3]上的最大值,最小值分别是 ( )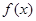 ,设其导函数
,设其导函数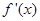 ,当
,当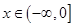 时,恒有
时,恒有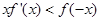 ,令
,令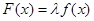 ,则满足
,则满足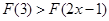 的实数x的取值范围是( )
的实数x的取值范围是( )