题目内容

求函数y=
sinx
+
-cosx
的定义域．
考点：余弦函数的单调性
专题：三角函数的图像与性质
分析：由函数的解析式可得，
sinx≥0
cosx≤0
，再根据正弦函数、余弦函数在各个象限中的符号，求得x的范围．
解答： 解：∵函数y=
sinx
+
-cosx
的，∴
sinx≥0
cosx≤0
，∴2kπ+
π
2
≤x≤2kπ+π，k∈z，
故函数的定义域为{x|2kπ+
π
2
≤x≤2kπ+π，k∈z}．
点评：本题主要考查正弦函数、余弦函数在各个象限中的符号，属于基础题．
练习册系列答案
相关题目
已知曲线C：x2+y2-2x-4y+m=0．
（1）当m为何值时，曲线C表示圆；
（2）在（1）的条件下，若曲线C与直线3x+4y-6=0交于M、N两点，且|MN|=3
3
，求m的值；
（3）在（1）的条件下，设直线x-y-1=0与圆C交于A，B两点，是否存在实数m，使得以AB为直径的圆过原点，若存在，求出实数m的值；若不存在，请说明理由．
已知函数f（x）=3sin（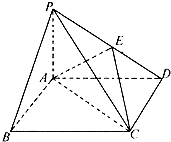
1
2
x-
π
4
）．x∈R．
（1）列表并画出函数f（x）在长度为一个周期的闭区间上的简图；
（2）将函数y=sinx的图象作怎样的变换可得到f（x）的图象？
已知可由数列{an}构造一列向量：
βn
=（2an，an+1-2n+1），n∈Z+．又向量
m
=（1，3），
p
=（3a1，7-a2），且向量
m
与
p
垂直，以及向量
m
与
βn
平行（n∈Z+）．
（1）试确定a1的值；
（2）求数列{an}的通项公式．
设△ABC的内角A，B，C的对边分别为a，b，c，则总有a+b＞c．由正弦定理得sinA+sinB＞sinC．由导数公式：（sinx）′=cosx，可以得到结论：对任意△ABC有cosA+cosB＞cosC．上述结论是否正确？如果不正确，请举出反例，并指出推导过程中的错误．
已知一个扇形的周长是6cm，该扇形的中心角是1弧度，求该扇形的面积．
已知sin（
π
4
-α）=-
4
5
，sin（
3π
4
+β）=
5
13
，且α∈（
π
4
，
3π
4
），β∈（0，
π
4
），求sin（α-β）的值．
四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，E是侧棱PD的中点．
（1）求证：PB∥平面ACE；
（2）求证：PA⊥平面ABCD．
设函数f（x）=sin（
πx
4
-
π
6
）-2cos2
πx
8
+1．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）若函数y=g（x）与y=f（x）的图象关于直线x=1对称，求当x∈[0，
4
3
]时y=g（x）的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网