题目内容
已知等差数列{an}中,a3+a6=17,a1a8=-38且a1<a8.
(Ⅰ)求{an}的通项公式;
(Ⅱ)调整数列{an}的前三项a1,a2,a3的顺序,使它成为等比数列{bn}的前三项,求{bn}的通项公式.
(Ⅰ)求{an}的通项公式;
(Ⅱ)调整数列{an}的前三项a1,a2,a3的顺序,使它成为等比数列{bn}的前三项,求{bn}的通项公式.
考点:等差数列的性质
专题:综合题,等差数列与等比数列
分析:(Ⅰ)由已知,得17=a3+a6=a1+a8,又a1a8=-38,a1<a8,求出首项与公差,即可求{an}的通项公式;
(Ⅱ)依题意可得:数列{bn}的前三项为b1=1,b2=-2,b3=4或b1=4,b2=-2,b3=1,即可求{bn}的通项公式.
(Ⅱ)依题意可得:数列{bn}的前三项为b1=1,b2=-2,b3=4或b1=4,b2=-2,b3=1,即可求{bn}的通项公式.
解答:
解:(Ⅰ)由已知,得17=a3+a6=a1+a8
又a1a8=-38,a1<a8,∴
=-2,
=19,
∴{an}的公差d=3…(3分)
∴an=3n-5…(6分)
(Ⅱ)由(Ⅰ),得a1=-2,a2=1,a3=4
依题意可得:数列{bn}的前三项为b1=1,b2=-2,b3=4或b1=4,b2=-2,b3=1
(i)当等比数列{bn}的前三项为b1=1,b2=-2,b3=4时,则公比q=-2,∴bn=(-1)n-12n-1…(9分)
(ii)当等比数列{bn}的前三项为b1=4,b2=-2,b3=1时,则公比q=-
.∴bn=(-1)n-123-n…(12分)
又a1a8=-38,a1<a8,∴
| a | 1 |
| a | 8 |
∴{an}的公差d=3…(3分)
∴an=3n-5…(6分)
(Ⅱ)由(Ⅰ),得a1=-2,a2=1,a3=4
依题意可得:数列{bn}的前三项为b1=1,b2=-2,b3=4或b1=4,b2=-2,b3=1
(i)当等比数列{bn}的前三项为b1=1,b2=-2,b3=4时,则公比q=-2,∴bn=(-1)n-12n-1…(9分)
(ii)当等比数列{bn}的前三项为b1=4,b2=-2,b3=1时,则公比q=-
| 1 |
| 2 |
点评:本题考查等差数列的通项与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目


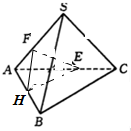 如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为
如图,一个四面体S-ABC的六条棱长都为4,E为SA的中点,过点E作平面EFH∥平面SBC.且平面EFH∩平面ABC=FH,则△HFE面积为