题目内容
2.设数列{an}是以2为首项,1为公差的等差数列,数列{bn}是以1为首项,2为公比的等比数列,则b${\;}_{{a}_{1}}$+b${\;}_{{a}_{2}}$+b${\;}_{{a}_{3}}$+…+b${\;}_{{a}_{6}}$=126.分析 由已知分别写出等差数列和等比数列的通项公式,求出a1至a7的值,则对应的b${\;}_{{a}_{1}}$至b${\;}_{{a}_{6}}$的值可求,答案可求.
解答 解:∵数列{an}是以2为首项,1为公差的等差数列,∴an=2+(n-1)×1=n+1.
则a1=2,a2=3,a3=4,a4=5,a5=6,a6=7,
{bn}是以1为首项,2为公比的等比数列,则bn=1×2n-1=2n-1,
∴b${\;}_{{a}_{1}}$+b${\;}_{{a}_{2}}$+b${\;}_{{a}_{3}}$+…+b${\;}_{{a}_{6}}$=b2+b3+b4+b5+b6+b7
=2+4+8+16+32+64=126.
故答案为:126
点评 本题考查了等差数列和等比数列的通项公式,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
12.函数y=|x|-1的图象是( )
| A. |  | B. |  | C. |  | D. |  |
12.已知函数f(x)=lnx+$\frac{1}{2}$ax2-2x有两个极值点,则a的取值范围是( )
| A. | (-∞,1) | B. | (0,2) | C. | (0,1) | D. | (0,3) |
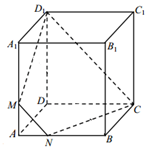 如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1
如图,已知正方体 ABCD-A1B1C1D1的棱长为3,M,N 分别是棱 AA1,AB上的点,且 AM=AN=1