题目内容
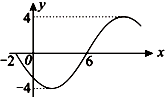
函数y=Asin(ωx+φ)(ω>0,|φ|<
,x∈R)的部分图象如图所示,则函数表达式( )
| π |
| 2 |

A、y=-4sin(
| ||||
B、y=4sin(
| ||||
C、y=-4sin(
| ||||
D、y=4sin(
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
解答:
解:由函数的解析式可得A=4,
=
=6+2,可得ω=
.
再根据sin[(-2)×
+φ]=0,可得(-2)×
+φ=kπ,k∈z,再结合|φ|<
,∴φ=
,
∴y=-4sin(
x+
),
故选:C.
| T |
| 2 |
| π |
| ω |
| π |
| 8 |
再根据sin[(-2)×
| π |
| 8 |
| π |
| 8 |
| π |
| 2 |
| π |
| 4 |
∴y=-4sin(
| π |
| 8 |
| π |
| 4 |
故选:C.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,属于基础题.

练习册系列答案
相关题目
数列{xn}对任意n∈N*满足(1+xn)(1-xn+1)=2,且x1=2,则x2013•x2015的值为( )
| A、2 | B、1 | C、0 | D、-1 |
若函数f(x)=5loga(3x-8)+1(a>0,且a≠1),则f(x)过定点( )
| A、(1,3) |
| B、(1,1) |
| C、(5,1) |
| D、(3,1) |
已知偶函数f(x)在[0,2]内单调递减,若a=f(-1),b=f(log
),c=f(lg0.5),则a、b、c之间的大小关系是( )
| 1 |
| 2 |
| 1 |
| 4 |
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、c>a>b |
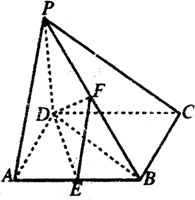 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是PB,AB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是PB,AB的中点. 随着社会的发展,网上购物已成为一种新型的购物方式.某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价.以下为四款商品销售情况的条形图和用分层抽样法选取100份评价的统计表:
随着社会的发展,网上购物已成为一种新型的购物方式.某商家在网上新推出A,B,C,D四款商品,进行限时促销活动,规定每位注册会员限购一件,并需在网上完成对所购商品的质量评价.以下为四款商品销售情况的条形图和用分层抽样法选取100份评价的统计表: