题目内容
过三角形OAB的重心G的直线L分别与边OA,OB交于点P,Q,已知
=m倍的
,
=n倍的
,则( )
| OP |
| OA |
| OQ |
| OB |
A、m+n=
| ||||||
B、m+n=
| ||||||
C、
| ||||||
D、
|
考点:向量在几何中的应用
专题:平面向量及应用
分析:根据三角形重心的性质,得
=
+
,进而得到
关于向量
、
的表达式,再根据已知条件得
关于向量
、
的表达式,利用向量共线的条件列式,化简整理可得本题的答案.
| OG |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| GP |
| OA |
| OB |
| PQ |
| OA |
| OB |
解答:
解: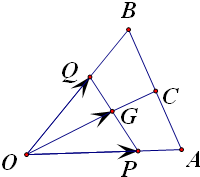 ∵G是△OAB的重心,
∵G是△OAB的重心,
∴点G在△OAB的中线OC上,且
=
,
∵
=
(
+
),
∴
=
×
(
+
)=
+
,
∵
=m
,
=n
,
∴
=
-
=n
-m
,
又∵
=
-
=(m-
)
-
,
、
是共线向量
∴(m-
)×n=(-m)×(-
),
整理得
+
=3,
故选:D
 ∵G是△OAB的重心,
∵G是△OAB的重心,∴点G在△OAB的中线OC上,且
| OG |
| 2 |
| 3 |
| OC |
∵
| OC |
| 1 |
| 2 |
| OA |
| OB |
∴
| OG |
| 2 |
| 3 |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
∵
| OP |
| OA |
| OQ |
| OB |
∴
| PQ |
| OQ |
| OP |
| OB |
| OA |
又∵
| GP |
| OP |
| OG |
| 1 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| GP |
| PQ |
∴(m-
| 1 |
| 3 |
| 1 |
| 3 |
整理得
| 1 |
| m |
| 1 |
| n |
故选:D
点评:本题以三角形的重心为载体,求满足条件的一个等式,着重考查了三角形重心的性质和平面向量基本定理等知识,属于基础题.

练习册系列答案
相关题目
当a=3时,如图所示的程序段输出的结果是( )


| A、6 | B、7 | C、10 | D、9 |
设集合U={1,2,3,4,5},A={1,3,5},B={2,3,5},则图中阴影部分表示的集合是( )
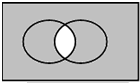

| A、{1,2,4} | B、{4} |
| C、{3,5} | D、∅ |
已知全集M={x||2x-1|≤1,x∈Z},集合N={3,a},若M∩N≠∅,则a等于( )
| A、1 | B、2 | C、1或2 | D、0或1 |