已知(1-x)10=a0+a1(1+x)+a2(1+x)2+-+a10(1+x)10.则a9=( )A．-20B．20C．-10D．10 题目和参考答案——青夏教育精英家教网——

题目内容

12．已知（1-x）¹⁰=a₀+a₁（1+x）+a₂（1+x）²+…+a₁₀（1+x）¹⁰，则a₉=（　　）

A．

-20

B．

20

C．

-10

D．

10

分析由（1-x）¹⁰=（x-1）¹⁰=[（1+x）-2]¹⁰，按二项式展开式，求出a₉的值即可．

解答解：∵（1-x）¹⁰=（x-1）¹⁰=[（1+x）-2]¹⁰=a₀+a₁（1+x）+a₂（1+x）²+…+a₁₀（1+x）¹⁰，
a₉是展开式的第10项的系数，所以a₉=（-2）¹C₁₀⁹=-20．
故选：A

点评本题考查了二项式定理的灵活应用问题，也考查了计算能力与逻辑思维能力，是基础题目．

练习册系列答案

快乐AB卷系列答案

轻松赢考期末卷系列答案

全优期末大考卷系列答案

一通百通考点预测期末测试卷系列答案

冲刺100分全程密卷系列答案

成龙计划课时一本通系列答案

名师导学系列答案

南通密卷系列答案

培优计划赢在起跑线系列答案

情景导学系列答案

相关题目

2．已知函数f（x）=asinx+bx³+1（a，b∈R），f′（x）为f（x）的导函数，则f（2016）+f（-2016）+f′（2017）-f′（-2017）=（　　）

3．证明：a²+b²+c²=ab+bc+ca的充要条件是△ABC为等边三角形．这里a，b，c是△ABC的三条边．

20．已知向量$\overrightarrow a$=（{cosx，-$\sqrt{3}$cosx），$\overrightarrow b$=（cosx，sinx），函数f（x）=$\overrightarrow a$•$\overrightarrow b$+1．
（Ⅰ）求函数f（x）的单调递增区间；
（Ⅱ）若f（θ）=$\frac{5}{6}$，$θ∈（\frac{π}{3}，\frac{2π}{3}），求sin2θ$的值．

7．为了解重庆某社区居民的家庭年收入和年支出的关系，随机调查了5户家庭，得到统计数据表，根据表中可得回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其中$\stackrel{∧}{b}$=0.5，据此估计，该社区一户收入为16万元家庭年支出为（　　）

收入x（万元）	6	8	10	12	14
支出y（万元）	6	7	8	9	10

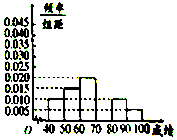如图是从成都某中学参加高三体育考试的学生中抽出的40名学生体育成绩（均为整数）的频率分布直方图，该直方图恰好缺少了成绩在区间[70，80）内的图形，根据图形的信息，回答下列问题：
（1）求成绩在区间[70，80）内的频率，并补全这个频率分布直方图，并估计这次考试的及格率（60分及以上为及格）；
（2）从成绩在[80，100]内的学生中选出三人，记在90分以上（含90分）的人数为X，求X的分布列及数学期望．

4．已知函数F（x）与f（x）=lnx的图象关于直线y=x对称．
（Ⅰ）不等式xf（x）≥ax-1对任意x∈（0，+∞）恒成立，求实数a的最大值；
（Ⅱ）设f（x）F（x）=1在（1，+∞）内的实根为x₀，m（x）=$\left\{\begin{array}{l}{xf（x），1＜x≤{x}_{0}}\\{\frac{x}{F（x）}，x＞{x}_{0}}\end{array}\right.$，若在区间（1，+∞）上存在m（x₁）=m（x₂）（x₁＜x₂），证明：$\frac{{x}_{1}+{x}_{2}}{2}$＞x₀．

1．已知函数f（x）=$\frac{{e}^{x+b}}{x}$过点（1，e）．
（1）求y=f（x）的单调区间；
（2）当x＞0时，求$\frac{f（x）}{x}$的最小值；
（3）试判断方程f（x）-mx=0（m∈R且m为常数）的根的个数．

体积为18$\sqrt{3}$的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上，球心O在此三棱锥内部，且R：BC=2：3，点E为线段BD上一点，且DE=2EB，过点E作球O的截面，则所得截面圆面积的取值范围是[8π，16π]．