题目内容
2.若不等式x2<|x-1|+a在区间(-3,3)上恒成立,则实数a的取值范围为[7,+∞).分析 分离参数得a>x2-|x-1|,求出右侧分段函数在(-3,3)上的最值即可得出a的范围.
解答 解:由x2<|x-1|+a得a>x2-|x-1|,
令f(x)=x2-|x-1|=$\left\{\begin{array}{l}{{x}^{2}-x+1,1≤x<3}\\{{x}^{2}+x-1,-3<x<1}\end{array}\right.$,
∴f(x)在(-3,-$\frac{1}{2}$]上单调递减,在(-$\frac{1}{2}$,3)上单调递增,
∵f(-3)=5,f(3)=7,
∴f(x)<7,
∴a的取值范围是[7,+∞).
故答案为[7,+∞).
点评 本题考查了函数的单调性与最值的计算,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知实数x,y满足x2+4y2≤4,则|x+2y-4|+|3-x-y|的最大值为( )
| A. | 6 | B. | 12 | C. | 13 | D. | 14 |
12.甲乙和其他4名同学合影留念,站成两排三列,且甲乙两人不在同一排也不在同一列,则这6名同学的站队方法有( )
| A. | 144种 | B. | 180种 | C. | 288种 | D. | 360种 |
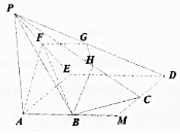 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于G,H两点.