题目内容
7.在Rt△ABC中,A=$\frac{π}{2}$,AB=2,AC=2$\sqrt{3}$,线段EF在斜边BC上运动,且EF=1,设∠EAF=θ,则tanθ的取值范围是[$\frac{\sqrt{3}}{9}$,$\frac{4\sqrt{3}}{11}$].分析 如图建立直角坐标系,设BF=k,k∈[0,3].得F(2-$\frac{1}{2}k$,$\frac{\sqrt{3}}{2}k$),E($\frac{3}{2}-\frac{1}{2}k$,$\frac{\sqrt{3}}{2}(k+1)$).
tan∠EAB=$\frac{\sqrt{3}(k+1)}{3-k}$,tan∠FAB=$\frac{\sqrt{3}k}{4-k}$,.tanθ=tan(∠EAB-∠FAB)=$\frac{\sqrt{3}}{{k}^{2}-k+3}$;即可求取值范围.
解答 解:如图建立直角坐标系,设BF=k,k∈[0,3].
∴∠B=60°,∴F(2-$\frac{1}{2}k$,$\frac{\sqrt{3}}{2}k$),E($\frac{3}{2}-\frac{1}{2}k$,$\frac{\sqrt{3}}{2}(k+1)$).
∴tan∠EAB=$\frac{\sqrt{3}(k+1)}{3-k}$,tan∠FAB=$\frac{\sqrt{3}k}{4-k}$,.
tanθ=tan(∠EAB-∠FAB)=$\frac{\sqrt{3}}{{k}^{2}-k+3}$;
∵k∈[0,3].∴${k}^{2}-k+3∈[\frac{11}{4},9]$,tanθ的取值范围是[$\frac{\sqrt{3}}{9},\frac{4\sqrt{3}}{11}$]
故答案为[$\frac{\sqrt{3}}{9},\frac{4\sqrt{3}}{11}$].
点评 本题考查了建立坐标系解决平面几何问题,属于难题.

练习册系列答案
相关题目
18.设集合M={x|x≥2},N={x|x2-6x+5<0},则M∩N=( )
| A. | (1,5) | B. | [2,5) | C. | (1,2] | D. | [2,+∞) |
19.执行下面的程序框图,输出S的值为( )


| A. | 8 | B. | 18 | C. | 26 | D. | 80 |
16.用半径为R的圆铁皮剪一个内接矩形,再以内接矩形的两边分别作为圆柱的高与底面半径,则圆柱的体积最大时,该圆铁皮面积与其内接矩形的面积比为( )
| A. | $\frac{3\sqrt{3}π}{8}$ | B. | $\frac{3\sqrt{3}π}{7}$ | C. | $\frac{3\sqrt{2}π}{8}$ | D. | $\frac{3\sqrt{2}π}{7}$ |
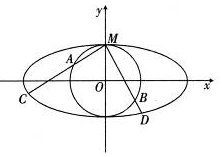 如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1).
如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1).