题目内容
将容量为n的样本中的数据分成5组，绘制频率分布直方图．若第1至第5个长方形的面积之比3：4：5：2：1，且最后两组数据的频数之各等于15，则n等于 ．
考点：频率分布直方图
专题：概率与统计
分析：根据频率和为1，求出直方图中最后两组数据的频率之和，再根据频率、频数与样本容量的关系，求出样本容量．
解答：
解：根据频率和为1，得；
直方图中最后两组数据的频率之和为
=
对应的频数为15，
∴样本容量为n=
=75．
故答案为：75．
直方图中最后两组数据的频率之和为
| 2+1 |
| 3+4+5+2+1 |
| 1 |
| 5 |
对应的频数为15，
∴样本容量为n=
| 15 | ||
|
故答案为：75．
点评：本题考查了频率、频数与样本容量的关系，是基础题目．
练习册系列答案
相关题目
设函数f（x）=sin（ωx+φ）+cos（ωx+φ）（ω＞0，|φ|＜
）的最小正周期为π，且f（-x）=f（x），则（ ）
| π |
| 2 |
A、f（x）在（0，
| ||||
B、f（x）在（
| ||||
C、f（x）在（
| ||||
D、f（x）在（
|
已知函数f（x）=
+xlnx，则曲线y=f（x）在x=1处的切线方程为（ ）
| 2 |
| x |
| A、x-y-3=0 |
| B、x-y+3=0 |
| C、x+y-3=0 |
| D、x+y+3=0 |
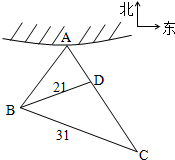如图所示，近日我渔船编队在岛A周围海域作业，在岛A的南偏西20°方向有一个海面观测站B，某时刻观测站发现有不明船只向我渔船编队靠近，现测得与B相距31海里的C处有一艘海警船巡航，上级指示海警船沿北偏西40°方向，以40海里/小时的速度向岛A直线航行以保护我渔船编队，30分钟后到达D处，此时观测站测得B，D间的距离为21海里．