题目内容
1.观察下列三角形数表,数表(1)是杨辉三角数表,数表(2)是与数表(1)有相同构成规律(除每行首末两端的数外)的一个数表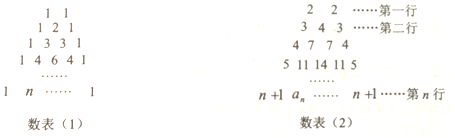
对于数表(2),设第n行第二个数为an(n∈N*)(如a1=2,a2=4,a3=7)
(I )归纳出an与an-1(n≥2,n∈N*)的递推公式(不用证明),并由归纳的递推公式,求出{an}的通项公式an
(Ⅱ)数列{bn}满足:(an-1)•bn=1,求证:b1+b1+…+bn<2.
分析 (Ⅰ)归纳an=an-1+n,利用迭代法即可求出通项公式,
(Ⅱ)求出bn=$\frac{1}{{a}_{n}-1}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n-1}$),利用裂项求和和放缩法即可证明.
解答 解:(Ⅰ)依题意当n≥2时可归纳an=an-1+n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1,a1=2,
∴an=n+(n-1)+…+2+2=$\frac{(n+2)(n-1)}{2}$+2=$\frac{1}{2}$(n2+n)+1,
检验当n=1时,上式成立,
∴{an}的通项公式an=$\frac{1}{2}$(n2+n)+1,
(Ⅱ)∵(an-1)•bn=1,
∴bn=$\frac{1}{{a}_{n}-1}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n-1}$),
∴b1+b1+…+bn=2(1-$\frac{1}{2}$+$\frac{1}{2}$$-\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n-1}$)]=2(-1$\frac{1}{n+1}$)<2
点评 本题考查数列的通项公式,数列求和,放缩法,证明不等式,考查计算能力.

练习册系列答案
相关题目
11.在数列{an}中,${a_1}=\frac{1}{2},{a_n}_{+1}=1-\frac{1}{a_n}$,则a5=( )
| A. | 2 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
12.设{an}是等差数列,下列结论中正确的是( )
| A. | 若a1+a2>0,则a2+a3>0 | B. | 若a1+a2<0,则a2+a3<0 | ||
| C. | 若0<a1<a2,则a2>$\sqrt{{a}_{1}{a}_{3}}$ | D. | 若a1<0,则(a2-a1)(a2-a3)<0 |
6.在△ABC中,内角A,B,C的对边分别为a,b,c,且sin2B+sin2C+sinBsinC-sin2A=0,则$\frac{asin(30°-C)}{b-c}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
3.假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其2×2列联表为:
对同一样本,以下数据能说明X与Y有关的可能性最大的一组为( )
(参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$)
| Y X | y1 | y2 | 总计 |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
(参考公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$)
| A. | a=5,b=4,c=3,d=2 | B. | a=5,b=3,c=4,d=2 | C. | a=2,b=3,c=4,d=5 | D. | a=3,b=2,c=4,d=5 |