题目内容
在△ABC中,已知AB=AC=5,BC=6,则
•
=( )
| AB |
| BC |
| A、18 | B、36 |
| C、-18 | D、-36 |
考点:平面向量数量积的运算
专题:计算题,解三角形,平面向量及应用
分析:运用余弦定理,求得cosB,再由向量的数量积的定义,计算即可得到.
解答:
解:由于AB=AC=5,BC=6,
则cosB=
=
,
则
•
=|
|•|
|•cos(π-B)=5×6×(-
)=-18.
故选C.
则cosB=
| 25+36-25 |
| 2×5×6 |
| 3 |
| 5 |
则
| AB |
| BC |
| AB |
| BC |
| 3 |
| 5 |
故选C.
点评:本题考查平面向量的数量积的定义,考查余弦定理的运用,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
设Sn是等差数列{an}的前n项和,已知a5=9,S2=4,则a2=( )
| A、1 | B、2 | C、3 | D、5 |
在△ABC中,
=(cos18°,sin18°),
=(2cos63°,2cos27°)则面积为( )
| AB |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设x,y满足约束条件
则z=x-2y的最小值为( )
|
| A、-10 | B、-6 | C、-1 | D、0 |
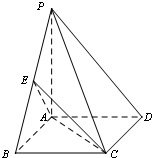 如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,点E为PB的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AB,点E为PB的中点.