题目内容
已知
=21，那么n= ．
| C | n-1 n+1 |
考点：组合及组合数公式
专题：排列组合
分析：根据组合数的公式，列出方程，求出n的值．
解答：
解：∵
=21，
∴
=21，
即
=21；
解得n=6或n=-7（舍去），
∴n的值是6．
故答案为：6．
| C | n-1 n+1 |
∴
| C | 2 n+1 |
即
| n(n+1) |
| 2 |
解得n=6或n=-7（舍去），
∴n的值是6．
故答案为：6．
点评：本题考查了组合数公式的应用问题，解题时应根据组合数公式进行解答，是基础题目．
练习册系列答案
天天向上口算本系列答案
相关题目
设（x-1）31（2x-1）1981=a0+a1x+a2x2+a3x3+…+a2012x2012，求：
（1）a1+a2+a3+…+a2012；
（2）a0+a1+2a2+3a3+…+2012a2012．
（1）a1+a2+a3+…+a2012；
（2）a0+a1+2a2+3a3+…+2012a2012．
| lim |
| △x→0 |
| f(x0+△x)-f(x0-△x) |
| 2△x |
A、
| ||
| B、f′（x0） | ||
| C、2f′（x0） | ||
| D、-f′（x0） |
若sin（180°+α）+cos（90°+α）=-a，则cos（270°-α）+2sin（360°-α）的值是（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
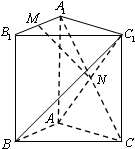三棱柱ABC-A1B1C1中，侧棱与底面垂直，∠ABC=90°，AB=BC=BB1，M是A1B1的中点，N是AC1与A1C的交点．