题目内容
已知函数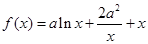 .
.
(1)若曲线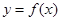 在点
在点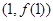 处的切线与直线
处的切线与直线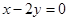 垂直,求实数
垂直,求实数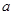 的值.
的值.
(2)若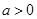 ,求
,求 的最小值
的最小值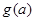 ;
;
(3)在(Ⅱ)上求证: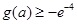 .
.
(Ⅰ)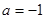 或
或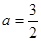 .
.
(Ⅱ)函数 在
在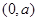 上单调递减,在
上单调递减,在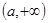 上单调递增;
上单调递增;
(Ⅲ)当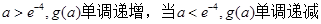
 。
。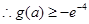 。
。
解析试题分析:(Ⅰ) 的定义域为
的定义域为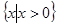 ,
,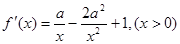 ,根据题意有
,根据题意有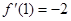 ,
,
所以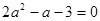 解得
解得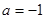 或
或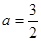 . 4分
. 4分
(Ⅱ)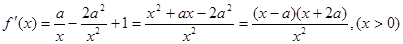
当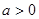 时,因为
时,因为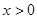 ,由
,由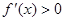 得
得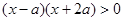 ,解得
,解得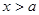 ,
,
由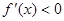 得
得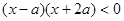 ,解得
,解得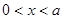 ,
,
所以函数 在
在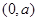 上单调递减,在
上单调递减,在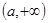 上单调递增; 8分
上单调递增; 8分
(Ⅲ)由(2)知,当a>0,  的最小值为
的最小值为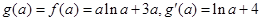
令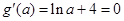
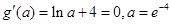
当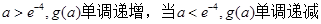
 。
。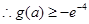 13分
13分
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性、最值及不等式的证明。
点评:典型题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。通过研究函数的单调区间、最值情况,得到证明不等式。涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

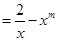 ,且
,且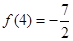
 的值
的值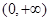 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明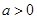 ,函数
,函数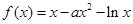 .
.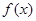 是单调函数,求实数
是单调函数,求实数 的取值范围;
的取值范围;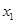 、
、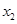 ,证明:
,证明: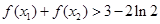 .
.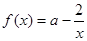 。
。 的奇偶性;
的奇偶性;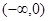 上的单调性并用定义证明。
上的单调性并用定义证明。 (a>0,且a≠1),
(a>0,且a≠1), =
= .
. 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标; 的图像过点(2,
的图像过点(2, ),证明:函数
),证明:函数 在
在 (1,2)上有唯一的零点.
(1,2)上有唯一的零点. 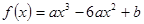 ,问是否存在实数
,问是否存在实数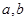 使
使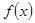 在
在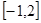 上取最大值3,最小值-29,若存在,求出
上取最大值3,最小值-29,若存在,求出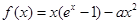
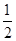 ,求f(x)的单调区间;
,求f(x)的单调区间;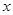 ≥0时f(x)≥0,求a的取值范围。
≥0时f(x)≥0,求a的取值范围。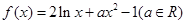
 的单调区间;
的单调区间;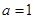 ,试分别解答以下两小题.
,试分别解答以下两小题.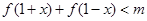 对任意的
对任意的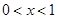 恒成立,求实数
恒成立,求实数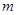 的取值范围;
的取值范围;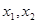 是两个不相等的正数,且
是两个不相等的正数,且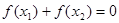 ,求证:
,求证: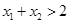 .
. .
. 的单调递增区间;
的单调递增区间; 的方程
的方程 在区间
在区间 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围.