题目内容
设函数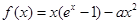
(Ⅰ)若a=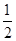 ,求f(x)的单调区间;
,求f(x)的单调区间;
(Ⅱ)若当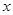 ≥0时f(x)≥0,求a的取值范围。
≥0时f(x)≥0,求a的取值范围。
(Ⅰ)
(Ⅱ)
解析试题分析:(I)


 6分
6分
(II)
令
若

若a>1,则当 为减函数,而
为减函数,而
从而当
综合得a的取值范围为 12分
12分
考点:本小题主要考查利用导数考查函数的单调性和单调性的应用.
点评:导数是研究函数性质是有力工具,利用导数研究函数单调性的前提是要注意函数的定义域,而且解决此类问题一般离不开分类讨论,讨论时要做到不重不漏.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

 .
.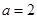 时,求
时,求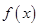 的极值;
的极值;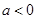 时,讨论
时,讨论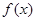 的单调性;
的单调性;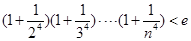 (
(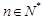 ,
,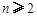 ,其中无理数
,其中无理数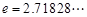 )
) .
.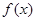 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;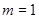 ,
,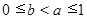 时,证明:
时,证明: .
.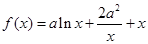 .
.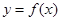 在点
在点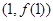 处的切线与直线
处的切线与直线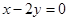 垂直,求实数
垂直,求实数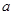 的值.
的值.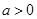 ,求
,求 的最小值
的最小值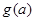 ;
;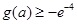 .
.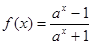 (a>1).
(a>1).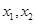 是函数
是函数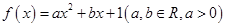 的两个零点,函数
的两个零点,函数 的最小值为
的最小值为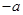 ,记
,记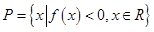
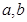 );
); 在什么范围内,函数
在什么范围内,函数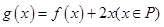 存在最小值?
存在最小值?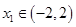 ,试确定
,试确定 的取值范围。
的取值范围。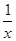 在(0,1)上是减函数.
在(0,1)上是减函数.

 时的值域;
时的值域; 
 )上存在极值,其中a>0,求实数a的取值范围;
)上存在极值,其中a>0,求实数a的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。