题目内容
已知函数
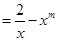 ,且
,且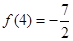
(1)求 的值
的值
(2)判断 在
在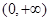 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明
(1)
(2)设变量,作差,变形,定号,下结论, 在
在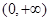 上单调递减
上单调递减
解析试题分析:解:(1)

 4分
4分
(2)
 在
在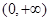 上单调递减 5分
上单调递减 5分
证明如下:
任取 ,则
,则
 =
= =
= 8分
8分
∵
∴
∴
 >0,即
>0,即
∴ 在
在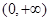 上单调递减 12分
上单调递减 12分
考点:函数的单调性
点评:解决的关键是能根据函数单调性的定义来加以证明,同时求解函数值,属于基础题。

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
题目内容
已知函数
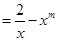 ,且
,且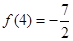
(1)求 的值
的值
(2)判断 在
在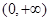 上的单调性,并利用定义给出证明
上的单调性,并利用定义给出证明
(1)
(2)设变量,作差,变形,定号,下结论, 在
在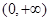 上单调递减
上单调递减
解析试题分析:解:(1)

 4分
4分
(2)
 在
在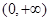 上单调递减 5分
上单调递减 5分
证明如下:
任取 ,则
,则
 =
= =
= 8分
8分
∵
∴
∴
 >0,即
>0,即
∴ 在
在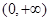 上单调递减 12分
上单调递减 12分
考点:函数的单调性
点评:解决的关键是能根据函数单调性的定义来加以证明,同时求解函数值,属于基础题。

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案