题目内容
已知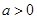 ,函数
,函数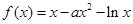 .
.
(1)若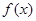 是单调函数,求实数
是单调函数,求实数 的取值范围;
的取值范围;
(2)若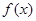 有两个极值点
有两个极值点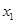 、
、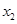 ,证明:
,证明: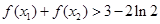 .
.
(1)
 (2)构造函数,利用单调性即得证.
(2)构造函数,利用单调性即得证.
解析试题分析:(1)
 ,则关于
,则关于 的方程
的方程 的判别式
的判别式
 ,
, 函数
函数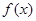 在
在 上单调递减
上单调递减 

 ,
, ,
, ,
, ,
,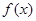 不是单调函数,
不是单调函数, ,
,

 , 且
, 且 是方程
是方程 的两正根,则
的两正根,则 ,
,

 ,
,
 ,
,
考点:利用导数研究函数的极值.
点评:本题考查了导数在解决函数极值和证明不等式中的应用,解题时要认真求导,防止错到起
点,还要有数形结合的思想,提高解题速度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
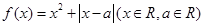 .
.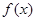 的奇偶性;
的奇偶性;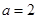 时,求
时,求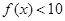 对
对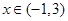 恒成立,求实数
恒成立,求实数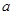 的取值范围.
的取值范围.
 .
.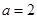 时,求
时,求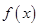 的极值;
的极值;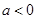 时,讨论
时,讨论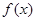 的单调性;
的单调性;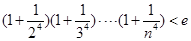 (
(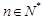 ,
,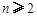 ,其中无理数
,其中无理数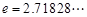 )
)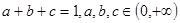 ,求证:
,求证: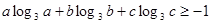 ;
;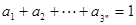 ,
,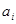 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: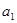
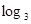
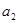
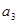
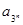
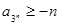
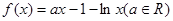
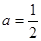 时,求函数在
时,求函数在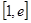 上的最大值和最小值;
上的最大值和最小值;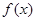 在
在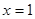 处取得极值,不等式
处取得极值,不等式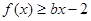 对
对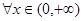 恒成立,求实数
恒成立,求实数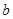 的取值范围。
的取值范围。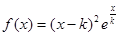 .
. 的单调区间;
的单调区间;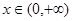 ,有
,有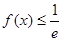 恒成立,求
恒成立,求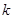 的取值范围.
的取值范围. .
.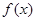 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;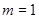 ,
,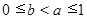 时,证明:
时,证明: .
.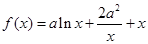 .
.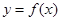 在点
在点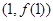 处的切线与直线
处的切线与直线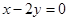 垂直,求实数
垂直,求实数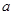 的值.
的值.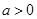 ,求
,求 的最小值
的最小值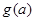 ;
;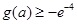 .
.

 时的值域;
时的值域;