题目内容
16．
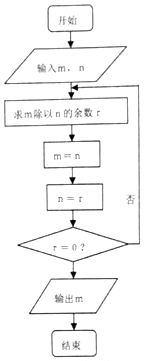如图程序框图的算法思路源于欧几里得名著《几何原本》中的“辗转相除法”，执行该程序框图，若输入m，n分别为225、135，则输出的m=（ ）| A． | 5 | B． | 9 | C． | 45 | D． | 90 |
分析 模拟程序框图的运行过程，该程序执行的是欧几里得辗转相除法，求出运算结果即可．
解答 解：模拟程序框图的运行过程，如下；
m=225，n=135，225÷135=1…90，r=90，不满足退出循环的条件；
m=135，n=90，135÷90=1…45，r=45不满足退出循环的条件
m=90，n=45，90÷45=2…0，r=0满足退出循环的条件
故输出m=45．
故选：C
点评 本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的答案，是基础题．
练习册系列答案
华东师大版一课一练系列答案
相关题目
6．从一批苹果中随机抽取100个作为样本，其重量（单位：克）的频数分布表如下：
（1）在频率分布直方图中，求分组重量在[85，95）对应小矩形的高；
（2）利用频率估计这批苹果重量的平均数．
（3）用分层抽样的方法从重量在[85，95）和[105，115）的苹果中抽取5个，从这5个苹果任取2个，求重量在这两个组中各有1个的概率．
| 分组（重量） | [75，85） | [85，95） | [95，105） | [105，115） |
| 频数（个） | 15 | 30 | 35 | 20 |
（2）利用频率估计这批苹果重量的平均数．
（3）用分层抽样的方法从重量在[85，95）和[105，115）的苹果中抽取5个，从这5个苹果任取2个，求重量在这两个组中各有1个的概率．
4．
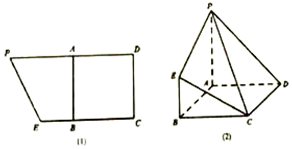已知梯形CEPD如图（1）所示，其中PD=8，CE=6，A为线段PD的中点，四边形ABCD为正方形，现沿AB进行折叠，使得平面PABE⊥平面ABCD，得到如图（2）所示的几何体．已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$（0＜λ＜1）时，平面DEF⊥平面PCE，则λ的值为（ ）
已知梯形CEPD如图（1）所示，其中PD=8，CE=6，A为线段PD的中点，四边形ABCD为正方形，现沿AB进行折叠，使得平面PABE⊥平面ABCD，得到如图（2）所示的几何体．已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$（0＜λ＜1）时，平面DEF⊥平面PCE，则λ的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
3．函数f（x）=x3+x-2有 （ ）个零点．
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
7．
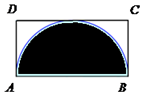若将一个质点随机投入如图所示的长方形ABCD中，其中AB=2，BC=1，则质点落在以AB为直径的半圆内的概率是（ ）
若将一个质点随机投入如图所示的长方形ABCD中，其中AB=2，BC=1，则质点落在以AB为直径的半圆内的概率是（ ）| A． | $\frac{π}{8}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{5}$ | D． | $\frac{π}{2}$ |