题目内容
18.从圆x2+y2-2x-2y+1=0外一点P(3,2)向这个圆作两条切线,则两条切线夹角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 0 |
分析 先求圆心到P的距离,再求两切线夹角一半的三角函数值,然后求出结果.
解答 解:圆x2+y2-2x-2y+1=0的圆心为M(1,1),半径为1,从外一点P(3,2)向这个圆作两条切线,
则点P到圆心M的距离等于$\sqrt{5}$,每条切线与PM的夹角的正切值等于$\frac{1}{2}$,
所以两切线夹角的正切值为tanθ=$\frac{2•\frac{1}{2}}{1-\frac{1}{4}}$=$\frac{4}{3}$,该角的余弦值等于$\frac{3}{5}$,
故选:B.
点评 本题考查圆的切线方程,两点间的距离公式,是基础题.

练习册系列答案
相关题目
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴长为2,离心率为$\sqrt{5}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{16}$=1 | B. | x2-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{2}$$-\frac{{y}^{2}}{3}$=1 | D. | x2$-\frac{{y}^{2}}{6}$=1 |
15.中国古代数学有着很多令人惊叹的成就.北宋沈括在《梦溪笔谈》卷十八《技艺》篇中首创隙积术.隙积术意即:将木捅一层层堆放成坛状,最上一层长有a个,宽有b个,共计ab个木桶.每一层长宽各比上一层多一个,共堆放n层,设最底层长有c个,宽有d个,则共计有木桶$\frac{n[(2a+c)b+(2c+a)d+(d-b)]}{6}$个.假设最上层有长2宽1共2个木桶,每一层的长宽各比上一层多一个,共堆放15层.则木桶的个数为( )
| A. | 1260 | B. | 1360 | C. | 1430 | D. | 1530 |
3.甲、乙两人相约周六上午8:00到8:30之间在公交车站乘车去新华书店,先到者若等了15分钟还没有等到对方,则需发微信联系.假设两人的出发时间是独立的,在8:00到8:30之间到达车站的时间是等可能的,则两人不需要发微信联系就能见面的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
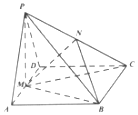 已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P的底面ABCD的射影,N是PC的中点.
已知四棱锥P-ABCD的底面ABCD是菱形,∠ADC=120°,AD的中点M是顶点P的底面ABCD的射影,N是PC的中点.