题目内容
设函数y=ln（cosx），x∈（-
，
）的图象是（ ）
| π |
| 2 |
| π |
| 2 |
A、 |
B、 |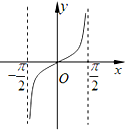
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：根据三角形函数的值域得到0＜cosx＜1，再根据对数函数的性质，得到ln（cosx）＜0，问题得以解决
解答：
解：∵x∈（-
，
），
∴0＜cosx＜1，
∵函数y=lnx为增函数，ln1=0
∴ln（cosx）＜0，
故选：A
| π |
| 2 |
| π |
| 2 |
∴0＜cosx＜1，
∵函数y=lnx为增函数，ln1=0
∴ln（cosx）＜0，
故选：A
点评：本题主要考查了三角形函数和对数函数的单调性，属于基础题
练习册系列答案
相关题目
已知a=53，b=52，c=54，则a，b，c三者的大小关系是（ ）
| A、b＞a＞c |
| B、c＞a＞b |
| C、a＞b＞c |
| D、b＞c＞a |
式子log327的值为（ ）
| A、9 | B、18 | C、2 | D、3 |
如图所示，已知三棱锥P-ABC中，∠ACB=90°，BC=4，AB=20，D为AB的中点，且△PDB是等边三角形，PA⊥PC．