题目内容
已知函数f(x)=x2-2ax,g(x)=-x2-1,若函数f(x)与g(x)有两条公切线,且由四个切点组成的多边形的周长为6.则a 的值为 .
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:分别求出设出切点,点P(x1,x12-2ax1)和点Q(x2,-x22-1),求出导数,求出切线的斜率,得到切线方程,推出x1+x2=a,2x1x2=a2-1,则有2x12-2ax1+a2-1=0,再求y1+y2=-1-a2.由对称性,可得另一条公切线段P′Q′的中点与PQ中点重合,所以公切线段PQ和P′Q′互相平分.即有切点P'(x2,f(x2)),Q'(x1,
g(x1)),PQ和P′Q′围成一个平行四边形PP'QQ',则有|PP'|+|PQ'|=3,得到a的方程,解得即可.
g(x1)),PQ和P′Q′围成一个平行四边形PP'QQ',则有|PP'|+|PQ'|=3,得到a的方程,解得即可.
解答:
解:函数y=x2-2ax的导数y′=2x-2a,
曲线f(x)在点P(x1,x12-2ax1)的切线方程是:
y-(x12-2ax1)=(2x1-2a)(x-x1),
即y=(2x1-2a)x-x12①
函数y=-x2-1的导数y′=-2x,
曲线g(x)在点Q(x2,-x22-1)的切线方程是
即y-(-x22-1)=-2x2(x-x2).
y=-2x2x+x22-1.②
如果直线l是过P和Q的公切线,
则①式和②式都是l的方程,
2x1-2a=-2x2,-x12=x22-1,
即有x1+x2=a,2x1x2=a2-1,
则有2x12-2ax1+a2-1=0,
设一条公切线上切点为:P(x1,y1),Q(x2,y2).
y1+y2=x12-2ax1+(-x22-1)=2x12-2ax1-2=-1-a2.
线段PQ的中点为(
,
).
另一条公切线段P′Q′的中点也是(
,
).
所以公切线段PQ和P′Q′互相平分.
即有切点P'(x2,f(x2)),Q'(x1,g(x1)),
PQ和P′Q′围成一个平行四边形PP'QQ'
则有|PQ'|=|x12-2ax1-(-x22-1)|=|2-a2|,
|PP'|=
=
•
=
•
由|PQ'|+|PP'|=3,即
•
+|2-a2|=3,
解得,a2=
,即有a=±
.
故答案为:±
.
曲线f(x)在点P(x1,x12-2ax1)的切线方程是:
y-(x12-2ax1)=(2x1-2a)(x-x1),
即y=(2x1-2a)x-x12①
函数y=-x2-1的导数y′=-2x,
曲线g(x)在点Q(x2,-x22-1)的切线方程是
即y-(-x22-1)=-2x2(x-x2).
y=-2x2x+x22-1.②
如果直线l是过P和Q的公切线,
则①式和②式都是l的方程,
2x1-2a=-2x2,-x12=x22-1,
即有x1+x2=a,2x1x2=a2-1,
则有2x12-2ax1+a2-1=0,
设一条公切线上切点为:P(x1,y1),Q(x2,y2).
y1+y2=x12-2ax1+(-x22-1)=2x12-2ax1-2=-1-a2.
线段PQ的中点为(
| a |
| 2 |
| -1-a2 |
| 2 |
另一条公切线段P′Q′的中点也是(
| a |
| 2 |
| -1-a2 |
| 2 |
所以公切线段PQ和P′Q′互相平分.
即有切点P'(x2,f(x2)),Q'(x1,g(x1)),
PQ和P′Q′围成一个平行四边形PP'QQ'
则有|PQ'|=|x12-2ax1-(-x22-1)|=|2-a2|,
|PP'|=
| (x1-x2)2+(x12-2ax1-x22+2ax2)2 |
=
| 1+a2 |
| (x1+x2)2-4x1x2 |
| 1+a2 |
| 2-a2 |
由|PQ'|+|PP'|=3,即
| 1+a2 |
| 2-a2 |
解得,a2=
| 1 |
| 2 |
| ||
| 2 |
故答案为:±
| ||
| 2 |
点评:本题考查导数的运用:求切线方程,考查两点间的距离公式的运用,考查运算化简的能力,属于难题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
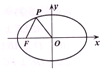 如图,已知椭圆C的中心为原点O,F(-2
如图,已知椭圆C的中心为原点O,F(-2| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知{an}、{bn}是两个等差数列,其中a1=3,b1=-3,且a19-b19=16,那么a10-b10的值为( )
| A、-6 | B、6 | C、0 | D、11 |
 已知△ABC中,∠BAC=90°,P为△ABC所在平面外一点,且PA=PB=PC,证明:平面PBC⊥平面ABC.
已知△ABC中,∠BAC=90°,P为△ABC所在平面外一点,且PA=PB=PC,证明:平面PBC⊥平面ABC.