题目内容
已知函数f(x)＝3ax＋1－2a，在(－1,1)上存在x0，使f(x0)＝0，则a的取值范围是( )
A．－1<a<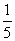
B．a>
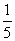
C．a<－1或a>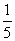 D．a<－1
C
[分析] a≠0时，f(x)为一次函数，故由x0∈(－1,1)时，f(x0)＝0知，f(－1)与f(1)异号．
[解析] 由题意得f(－1)·f(1)<0，
即(－3a＋1－2a)·(3a＋1－2a)<0，
即(5a－1)(a＋1)>0，∴a<－1或a>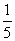.故选C.
练习册系列答案
名校课堂系列答案
相关题目
为{an}的“光阴”值，现知某数列的“光阴”值为Hn＝
，则数列{an}的通项公式为________．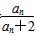
(n∈N*)．若bn＋1＝(n－λ)(
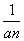＋1)(n∈N*)，b1＝－λ，且数列{bn}是单调递增数列，则实数λ的取值范围为( )
＋
的最小值为( )
B.
D.
＋a＋b(a、b为正实数)，若1⊙k<3，则k的取值范围为________．
)2>ab B．ac>bc
则使
·
取得最大值的点N的个数是( )