题目内容
已知数列{an}，{bn}满足a1＝1，且an、an＋1是函数f(x)＝x2－bnx＋2n的两个零点，则b10等于( )
A．24 B．32 C．48 D．64
D
[解析] 依题意有anan＋1＝2n，所以an＋1an＋2＝2n＋1，两式相除得
＝2，所以a1，a3，a5，…成等比数列，a2，a4，a6，…成等比数列，而a1＝1，a2＝2，所以a10＝2×24＝32，a11＝1×25＝32.又因为an＋an＋1＝bn，所以b10＝a10＋a11＝64，故选D.
练习册系列答案
相关题目
＝d(n∈N*，d为常数)，则称数列{an}为调和数列．已知数列{
}为调和数列，且x1＋x2＋…＋x20＝200，则x5＋x16＝________.
D.
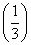n，把数列{an}的各项排列成如下的三角形状：
x，其中数列{an}是以4为首项的正项数列，则数列{an}的通项公式是________．
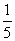B．a>