题目内容
10.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1的焦点在x轴上,以椭圆右顶点为焦点的抛物线标准方程为y2=16x.(1)求椭圆C的离心率
(2)若动直线l的斜率为$-\frac{{\sqrt{2}}}{2}$,且与椭圆C交于不同的两点M、N,已知点Q$(-\sqrt{2},0)$,求$\overrightarrow{QM}•\overrightarrow{QN}$的最小值.
分析 (1)y2=16x的焦点坐标为(4,0),所以a=4,可得c=$\sqrt{14}$,即可求出椭圆C的离心率;
(2)设直线l方程,与椭圆方程联立,消去y,再由根的判别式和韦达定理进行求解.
解答 解:(1)y2=16x的焦点坐标为(4,0),所以a=4,
所以c=$\sqrt{14}$,
所以椭圆C的离心率为$\frac{\sqrt{14}}{4}$;
(2)设直线l方程为y=-$\frac{\sqrt{2}}{2}$x+b.
与椭圆方程联立,消去y,整理得5x2-8$\sqrt{2}$bx+(8b2-16)=0
因为直线l与椭圆C交于不同两点,所以△=128b2-20(8b2-16)>0,
解得-$\sqrt{10}$<b<$\sqrt{10}$.
设M(x1,y1),N(x2,y2),则x1+x2=$\frac{8\sqrt{2}}{5}$b,x1x2=$\frac{8{b}^{2}-16}{5}$,
y1y2=(-$\frac{\sqrt{2}}{2}$x1+b)(-$\frac{\sqrt{2}}{2}$x2+b)=$\frac{{b}^{2}-8}{5}$,
所以$\overrightarrow{QM}•\overrightarrow{QN}$=(x1+$\sqrt{2}$,y1)•(x2+$\sqrt{2}$,y2)=x1x2+$\sqrt{2}$(x1+x2)+y1y2+2=$\frac{9{b}^{2}+16b-14}{5}$,
因为-$\sqrt{10}$<b<,所以当b=-$\frac{8}{9}$时,$\overrightarrow{QM}•\overrightarrow{QN}$取得最小值-$\frac{38}{9}$.
点评 本题考查直线和圆锥曲线的综合运用,考查椭圆的性质,考查直线与椭圆的位置关系,正确运用韦达定理是关键.

| A. | -1+(-1)=2 | B. | $\frac{1}{2}$+$\frac{1}{3}$=$\frac{1}{5}$ | ||
| C. | 23•2n-1=23n-3 | D. | $\frac{1}{101}$+$\frac{1}{202}$+$\frac{1}{303}$+$\frac{1}{606}$=$\frac{2}{101}$ |
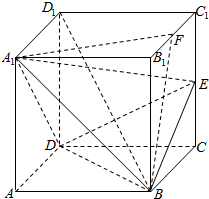 已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.
已知正方体ABCD-A1B1C1D1的棱长为2a,E为CC1的中点,F为B1C1的中点.(1)求证;BD⊥A1E;
(2)求证:平面A1BD⊥平面EBD;
(3)求证:平面A1BF⊥平面A1BD.
| A. | {0,1} | B. | {2,3,4,5} | C. | {0,2,3,4,5} | D. | {1,2,3,4,5} |
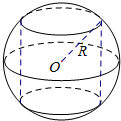 如图所示,半径R=2的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于8π.
如图所示,半径R=2的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的侧面积之差等于8π.