题目内容
12.已知函数$f(x)=\left\{\begin{array}{l}{2^x}-x,x>1\\ 1,x≤1\end{array}\right.$,则不等式$f(x)<f({\frac{2}{x}})$的解集是(0,$\sqrt{2}$).分析 求出x>1的导数,判断符号,可得f(x)在R上单调递增,讨论x>1,0<x≤1,x<0,得到不等式组,解不等式即可得到所求解集.
解答 解:函数$f(x)=\left\{\begin{array}{l}{2^x}-x,x>1\\ 1,x≤1\end{array}\right.$,
由x>1时,y=2x-x的导数为y′=2xln2-1,
2xln2-1>0,
可得f(x)在R上单调递增,
由不等式$f(x)<f({\frac{2}{x}})$,
可得当x>1时,x<$\frac{2}{x}$解得1<x<$\sqrt{2}$;
当0<x≤1时,x<$\frac{2}{x}$解得0<x≤1;
当x<0时,不等式$f(x)<f({\frac{2}{x}})$不成立.
综上可得,不等式$f(x)<f({\frac{2}{x}})$的解集是(0,$\sqrt{2}$).
故答案为:(0,$\sqrt{2}$).
点评 本题考查分段函数的运用:解不等式,注意运用导数判断单调性,考查分类讨论的思想方法,以及运算能力,属于中档题和易错题.

练习册系列答案
相关题目
3.已知双曲线3y2-mx2=3m(m>0)的一个焦点与抛物线y=$\frac{1}{8}$x2的焦点重合,则此双曲线的离心率为( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
4.设集合A={x|x2-2x-3<0},B={x||x-2|≤2},则A∩B=( )
| A. | (-1,0] | B. | [0,3) | C. | (3,4] | D. | (-1,3) |
1.已知i为虚数单位,则复数$z=\frac{1}{1-i}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
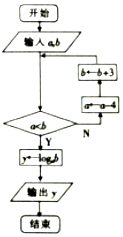 如图是一个算法的流程图,当输入a=10,b=2的时,输出的y值为3.
如图是一个算法的流程图,当输入a=10,b=2的时,输出的y值为3.