题目内容
17.已知函数f(x)=a(x+lnx)(a≠0),g(x)=x2.(1)若f(x)的图象在x=1处的切线恰好也是g(x)图象的切线.
①求实数a的值;
②若方程f(x)=mx在区间$[{\frac{1}{e},+∞})$内有唯一实数解,求实数m的取值范围.
(2)当0<a<1时,求证:对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|<|g(x1)-g(x2)|成立.
分析 (1)①求导数,利用f(x)的图象在x=1处的切线恰好也是g(x)图象的切线,求实数a的值;
②由x+lnx=mx,得m=1+$\frac{lnx}{x}$,设t(x)=1+$\frac{lnx}{x}$,x∈$[{\frac{1}{e},+∞})$,则问题等价于y=m与t(x)的图象在$[{\frac{1}{e},+∞})$上有唯一交点,即可求实数m的取值范围.
(2)设F(x)=f(x)-g(x),即F(x)=a(x+lnx)-x2,F(x)在[1,2]上单调递减,F′(x)=$\frac{ax+a-2{x}^{2}}{2}$≤0恒成立,即a≤$\frac{2{x}^{2}}{x+1}$在[1,2]上恒成立,即可证明结论.
解答 (1)解:①f′(x)=a(1+$\frac{1}{x}$),∴x=1,f′(x)=2a,切点为(1,a),
∴切线方程为y-a=2a(x-1),即y=2ax-a,
联立$\left\{\begin{array}{l}{y=2ax-a}\\{y={x}^{2}}\end{array}\right.$,消去y,可得x2-2ax+a=0,△=4a2-4a=0,∴a=1;
②由x+lnx=mx,得m=1+$\frac{lnx}{x}$,
设t(x)=1+$\frac{lnx}{x}$,x∈$[{\frac{1}{e},+∞})$,则问题等价于y=m与t(x)的图象在$[{\frac{1}{e},+∞})$上有唯一交点,
∵t′(x)=$\frac{1-lnx}{{x}^{2}}$,∴($\frac{1}{e}$,e),t′(x)>0,函数单调递增,(e,+∞),t′(x)<0,函数单调递减,
∵t($\frac{1}{e}$)=1-e,t(e)=1+$\frac{1}{e}$,且x∈(e,+∞)时,t(x)>1,
∴m∈[1-e]∪{1+$\frac{1}{e}$};
证明:(2)不妨设1≤x1<x2≤2,则f(x1)<f(x2),g(x1)<g(x2),
∴|f(x1)-f(x2)|<|g(x1)-g(x2)|可化为f(x2)-f(x1)<g(x2)-g(x1)
∴f(x2)-g(x2)<f(x1)-g(x1)
设F(x)=f(x)-g(x),即F(x)=a(x+lnx)-x2,∴F(x)在[1,2]上单调递减,
∴F′(x)=$\frac{ax+a-2{x}^{2}}{2}$≤0恒成立,即a≤$\frac{2{x}^{2}}{x+1}$在[1,2]上恒成立,
∵$\frac{2{x}^{2}}{x+1}$=$\frac{2}{(\frac{1}{x}+\frac{1}{2})^{2}-\frac{1}{4}}$≥1,∴a≤1,
从而,当0<a<1时,命题成立.
点评 本题考查导数知识的运用,考查多岁的几何意义,考查恒成立问题,属于中档题.

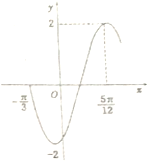 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位后的解析式为( )| A. | y=2sin(2x-$\frac{π}{6}$) | B. | y=2sin(2x+$\frac{π}{6}$) | C. | y=2sin(2x) | D. | y=2sin(2x+$\frac{π}{3}$) |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{5\sqrt{2}}{4}$ |