题目内容
设函数y=10
的图象是曲线C,曲线C1和C关于直线x=1对称,曲线C2和C1关于直线y=x对称,则C2的解析式为 .
| x |
| 2 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由函数解析式的方法易得C1的解析式,求反函数可得C2的解析式.
解答:
解:设P(x,y)为曲线C1上的任意一点,
则P关于x=1的对称点P′(2-x,y)在曲线C上,
∴y=10
,∴x=2-2lgy,
∴C1的反函数为y=2-2lgx,
∴C2的解析式为y=2-2lgx,
故答案为:y=2-2lgx
则P关于x=1的对称点P′(2-x,y)在曲线C上,
∴y=10
| 2-x |
| 2 |
∴C1的反函数为y=2-2lgx,
∴C2的解析式为y=2-2lgx,
故答案为:y=2-2lgx
点评:本题考查函数解析的求解和反函数,属基础题.

练习册系列答案
相关题目
P是椭圆
+
=1上一点,F1、F2分别是椭圆的左、右焦点,若|PF1|•|PF2|=12,则∠F1PF2的大小为( )
| x2 |
| 16 |
| y2 |
| 9 |
| A、30° | B、60° |
| C、120° | D、150° |
 如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40m的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,求AB的距离.
如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40m的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,求AB的距离.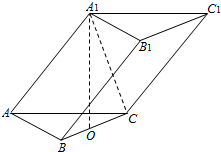 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=