题目内容
18.求下列函数的极值:y=x4-8x2+2.分析 求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的极值.
解答 解y′=4x3-16x,
令y′=0,解得x1=0,x2=2,x3=-2.
当x变化时,y′,y的变化情况如下表:
| x | (-∞,-2) | -2 | (-2,0) | 0 | (0,2) | 2 | (2,+∞) |
| y′ | - | 0 | + | 0 | - | 0 | + |
| y | 递减 | 极小值 -14 | 递增 | 极大值 2 | 递减 | 极小值 -14 | 递增 |
当x=±2时,y有极小值,y极小值=-14.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
14.复数$\frac{5}{2-i}$的共轭复数是( )
| A. | 2+i | B. | -2+i | C. | -2-i | D. | 2-i |
10.函数f(x)=x3-3ax2+3x有极小值,则a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a≥1或a≤-1 | D. | a>1或a<-1 |
8.△ABC中内角A,B,C的对边分别为a,b,c,若a,b,c成等比数列,且a2-c2=ac-bc,则角A的大小及$\frac{bsinB}{c}$的值分别为( )
| A. | $\frac{π}{6}$,$\frac{1}{2}$ | B. | $\frac{π}{3}$,$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{π}{3}$,$\frac{1}{2}$ | D. | $\frac{π}{6}$,$\frac{{\sqrt{3}}}{2}$ |
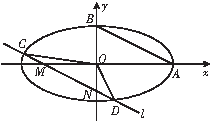 如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.
如图,A、B是离心率为$\frac{{\sqrt{3}}}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的两个顶点,且AB=$\sqrt{5}$.