题目内容
求函数y=2sin(
x-
)的对称轴和对称中心.
| 1 |
| 2 |
| π |
| 6 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由条件根据正弦函数的对称性,求得函数y=2sin(
x-
)的对称轴和对称中心.
| 1 |
| 2 |
| π |
| 6 |
解答:
解:对于函数y=2sin(
x-
),令
x-
=kπ+
,k∈z,求得x=2kπ+
,
故函数的对称轴方程为 x=2kπ+
,k∈z.
令
x-
=kπ,k∈z,求得x=2kπ+
,
故函数的对称中心为 (2kπ+
,0)k∈z.
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 4π |
| 3 |
故函数的对称轴方程为 x=2kπ+
| 4π |
| 3 |
令
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
故函数的对称中心为 (2kπ+
| 4π |
| 3 |
点评:本题主要考查正弦函数的对称性,属于基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠CAD=90°,PA⊥平面ABCD,PA=BC=1,AB=
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠CAD=90°,PA⊥平面ABCD,PA=BC=1,AB=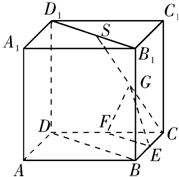 如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
如图所示,在正方体ABCD-A1B1C1D1中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证: