题目内容

8．双曲线$\frac{y^2}{9}-{x^2}=1$的实轴长是6，焦点坐标是$（0，±\sqrt{10}）$．

分析 双曲线$\frac{y^2}{9}-{x^2}=1$中，a=3，b=1，c=$\sqrt{10}$，即可求出双曲线$\frac{y^2}{9}-{x^2}=1$的实轴长，焦点坐标．

解答 解：双曲线$\frac{y^2}{9}-{x^2}=1$中，a=3，b=1，c=$\sqrt{10}$，
∴双曲线$\frac{y^2}{9}-{x^2}=1$的实轴长是2a=6，焦点坐标是$（0，±\sqrt{10}）$．
故答案为：6，$（0，±\sqrt{10}）$．

点评 本题考查双曲线的方程与性质，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
9．在数列{an}中，若a1=$\frac{1}{2}$，an=$\frac{1}{1-{a}_{n-1}}$（n≥2，n∈N），则a2012的值为（　　）
A．-1B．$\frac{1}{2}$C．1D．2
10．已知A点坐标为（-1，0），B点坐标为（1，0），且动点M到A点的距离是4，线段MB的垂直平分线l交线段MA于点P．（1）求动点P的轨迹C方程；
（2）若P是曲线C上的点，求k=|PA|•|PB|的最大值和最小值．
16．五名男同学，三名女同学外出春游，平均分成两组，每组4人，则女同学不都在同一组的不同分法有（　　）
A．30种B．65种C．35种D．70种
3．已知a、b、c为正数，
（1）若直线2x-（b-3）y+6=0与直线bx+ay-5=0互相垂直，试求2a+3b的最小值；
（2）求证：（ab+a+b+1）（ab+ac+bc+c2）≥16abc．
13．已知双曲线与椭圆$\frac{x^2}{36}+\frac{y^2}{27}=1$有相同的焦点，且虚轴的长为4．
（Ⅰ）求双曲线的方程；
（Ⅱ）求双曲线的渐近线方程．
20．已知数列{an}的前n项和为Sn，且Sn=2an-n，（n∈N*）．
（1）求证：数列{an+1}为等比数列；
（2）令bn=n+anlog2（an+1），求数列{bn}的前n项和Tn．
17．设x，y为实数，a，b（b＞0）为常数且满足：（x-2015）3+b（x-2015）+a=0，（y-2015）3+b（y-2015）=a，则x+y=4030．
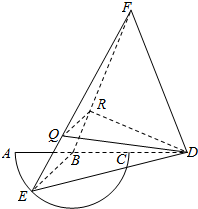18．如图，弧$\widehat{AEC}$是半径为a的半圆，AC为直径，点E为弧$\widehat{AC}$的中点，点B和点C为线段AD的三等分点，平面AEC外一点F满足FB=FD=$\sqrt{5}$a，FE=$\sqrt{6}$a．
（Ⅰ）证明：EB⊥FD；
（Ⅱ）已知点Q，R分别为线段FE，FB上的点，使得$\overrightarrow{FQ}$=λ$\overrightarrow{FE}$，$\overrightarrow{FR}$=λ$\overrightarrow{FB}$，求当RD最短时，平面BED与平面RQD所成二面角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网