题目内容
6.若x>0,$\frac{x}{5}$$+\frac{45}{x}$的最小值为6.分析 根据题意,结合基本不等式可得$\frac{x}{5}$$+\frac{45}{x}$≥2$\sqrt{\frac{x}{5}•\frac{45}{x}}$=6,分析等号成立的条件可得x=15时等号成立,即$\frac{x}{5}$$+\frac{45}{x}$的最小值为6,可得答案.
解答 解:根据题意,由x>0,
则$\frac{x}{5}$$+\frac{45}{x}$≥2$\sqrt{\frac{x}{5}•\frac{45}{x}}$=6,当且仅当$\frac{x}{5}$=$\frac{45}{x}$时,即x=15时等号成立,
即$\frac{x}{5}$$+\frac{45}{x}$的最小值为6;
故答案为:6.
点评 本题考查基本不等式的运用,解题时应注意是否满足不等式成立的条件.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
16.已知tan(π-α)=-2,则$\frac{sinα+cosα}{sinα-cosα}$=( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
1.长方体的相邻三个面的面积分别是12,15,20,且它的八个顶点都在同一个球面上,这个球的表面积是( )
| A. | 100π | B. | 60π | C. | 50π | D. | 30π |
9.tan(-$\frac{4π}{3}$)+tan$\frac{4π}{3}$等于( )
| A. | -2$\sqrt{3}$ | B. | -$\frac{2\sqrt{3}}{3}$ | C. | 0 | D. | $\frac{2\sqrt{3}}{3}$ |
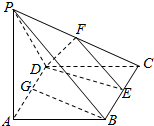 如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,
如图所示,在四棱柱P-ABCD中,底面ABCD是菱形,∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,