题目内容
12.已知:命题p:函数y=ax(a>0,且a≠1)为R上的单调递减函数,命题q:函数y=lg(ax2-x+a)值域为R,若“p且q”为假,求a的取值范围.分析 因为“p且q”为假命题,所以p真q假或p假q真或都为假命题.
解答 解:∵命题p:函数y=ax(a>0,且a≠1)为R上的单调递减函数,
∴0<a<1;
∵命题q:函数y=lg(ax2-x+a)值域为R,
∴△=≥0,
∴-$\frac{1}{2}$<a<$\frac{1}{2}$
若“p且q”为假,
所以:a≥$\frac{1}{2}$
点评 本题考查了“或”命题和“且”命题的真假性,关键是弄清两种命题的构成,及各部分的真假性.所有情况如下:
(1)p∧q为真的情况有:p真,且q真;p∧q为假的情况有:①p真,且q假,②p假,且q真,③p假,且q假,即“两真才真,一假为假”.
(2)p∨q为真的情况有:①p真,且q假,②p假,且q真,③p真,且q真;p∨q为假的情况有:p假,且q假,即“一真为真,两假才假”.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.给定集合An={1,2,3,…,n},n∈N*.若f是An→An的映射且满足:
①任取i,j∈An,若i≠j,则f(i)≠f(j);
②任取m∈An,若m≥2,则有m∈{f(1),f(2),…,f(m)}.
则称映射f为An→An的一个“优映射”.
例如:用表1表示的映射f:A3→A3是一个“优映射”.
表一
表2
(1)若f:A4→A4是一个“优映射”,请把表2补充完整(只需填出一个满足条件的映射);
(2)若f:A2015→A2015是“优映射”,且f(1004)=1,则f(1000)+f(1017)的最大值为2021.
①任取i,j∈An,若i≠j,则f(i)≠f(j);
②任取m∈An,若m≥2,则有m∈{f(1),f(2),…,f(m)}.
则称映射f为An→An的一个“优映射”.
例如:用表1表示的映射f:A3→A3是一个“优映射”.
表一
| i | 1 | 2 | 3 |
| F(i) | 2 | 3 | 1 |
| i | 1 | 2 | 3 | 4 |
| F(i) | 3 |
(2)若f:A2015→A2015是“优映射”,且f(1004)=1,则f(1000)+f(1017)的最大值为2021.
4.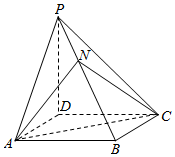 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与三棱锥D-PAC的体积比为( )| A. | 1:2 | B. | 1:8 | C. | 1:6 | D. | 1:3 |
1.已知函数f(x)=2016x+log2016($\sqrt{{x^2}+1$+x)-2016-x+2,则关于x的不等式f(3x+1)+f(x)>4的解集为( )
| A. | (-$\frac{1}{4}$,+∞) | B. | (-∞,-$\frac{1}{4}$) | C. | (0,+∞) | D. | (-∞,0) |