题目内容
在棱长为4的正方形ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP,点E在棱A1D1上,且A1D1=4ED1,求直线BE与平面APD1所成角的正弦值 .
考点:直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:建立坐标系求出
=(-3,-4,4),
=(-4,4,0),
=(-4,0,4),
设平面APD1的法向量为
=(x,y,z),得出平面APD1的法向量为
=(1,1,1),运用cos<
,
>=直线BE与平面APD1所成角的正弦值求解.
| BE |
| AP |
| AD1 |
设平面APD1的法向量为
| n |
| n |
| n |
| BE |
解答:
解:分别以DA,DC,DD1为x,y,z轴建立坐标系,
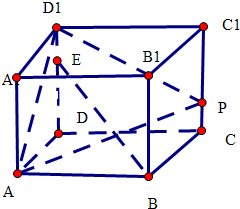
∵在棱长为4的正方形ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP,点E在棱A1D1上,且A1D1=4ED1,
∴B(4,4,0),E(1,0,4),A(4,0,0),P(0,4,0),D1(0,0,4),
∴
=(-3,-4,4),
=(-4,4,0),
=(-4,0,4),
设平面APD1的法向量为
=(x,y,z),
,x=y=z=1,
∴cos<
,
>=
=
,
故为
,
故答案为:

∵在棱长为4的正方形ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP,点E在棱A1D1上,且A1D1=4ED1,
∴B(4,4,0),E(1,0,4),A(4,0,0),P(0,4,0),D1(0,0,4),
∴
| BE |
| AP |
| AD1 |
设平面APD1的法向量为
| n |
|
|
∴cos<
| n |
| BE |
| -3 | ||||
|
| ||
| 41 |
故为
| ||
| 41 |
故答案为:
| ||
| 41 |
点评:本题考查了空间直线与平面所成的角的计算问题,运用平面的法向量求解,属于中档题,关键是求向量的坐标.

练习册系列答案
相关题目
确定结论“X与Y有关系”的可信度为99%时,则随即变量k2的观测值k必须( )
| A、大于10.828 |
| B、大于7.879 |
| C、大于6.635 |
| D、大于2.706 |
将周期为π的函数y=sin2ωx+2sinωxcosωx-cos2ωx(ω>0)的图象按
=(-
,1)平移后,所得函数图象的解析式为( )
| a |
| π |
| 8 |
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=1-
|
函数y=
在区间[3,6]上的最小值是( )
| 4 |
| x-2 |
| A、1 | B、3 | C、-2 | D、5 |
函数f(x)=Asin(ωx+ϕ)+k在一个周期内的图象如图,函数f(x)解析式为( )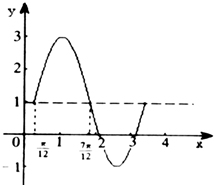

A、f(x)=4sin(
| ||||
B、f(x)=2sin(2x-
| ||||
C、f(x)=4sin(
| ||||
D、f(x)=2sin(2x-
|
己知关于x的方程(m+3)x2-4mx+2m-1=0 的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是( )
| A、-3<m<0 |
| B、0<m<3 |
| C、m<-3或m>0 |
| D、m<0 或 m>3 |
已知数列{an}中,a1=1,对所有n∈N*,都有a1a2…an=n2,则a3=( )
A、
| ||
| B、3 | ||
| C、9 | ||
D、
|