题目内容
9.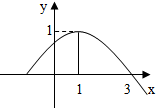 函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ≤2π)的部分图象如图所示,则( )
函数y=sin(ωx+φ)(x∈R,ω>0,0≤φ≤2π)的部分图象如图所示,则( )| A. | ω=$\frac{π}{2}$,φ=$\frac{π}{4}$ | B. | ω=$\frac{π}{3}$,φ=$\frac{π}{6}$ | C. | ω=$\frac{π}{4}$,φ=$\frac{π}{4}$ | D. | ω=$\frac{π}{4}$,φ=$\frac{5π}{4}$ |
分析 根据图象得出周期为8,代入特殊值计算φ.
解答 解:由函数图象可知函数的周期T=4×(3-1)=8,
即$\frac{2π}{ω}=8$,解得ω=$\frac{π}{4}$,
∵当x=1时,函数取得最大值,∴sin($\frac{π}{4}$+φ)=1,
∴$\frac{π}{4}$+φ=$\frac{π}{2}+2kπ$,解得φ=$\frac{π}{4}+2kπ$,
∵0≤φ≤2π,∴φ=$\frac{π}{4}$.
故选C.
点评 本题考查了正弦函数的图象与性质,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4.已知△ABC是一个圆锥的底面圆的内接三角形,AB=3,∠ACB=60°,母线与底面所成角的余弦值为$\frac{3}{5}$,则该圆锥的体积为( )
| A. | 8π | B. | 5π | C. | $\frac{4\sqrt{3}}{3}$π | D. | 4$\sqrt{3}$π |
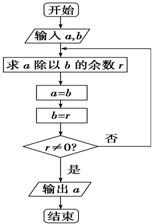 我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.
我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与古老的算法--“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a=6102,b=2016时,输出的a=18.