题目内容
在平面直角坐标系xOy中,设点F(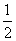 ,0),直线l:x=-
,0),直线l:x=-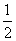 ,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
,点P在直线l上移动,R是线段PF与y轴的交点,RQ⊥FP,PQ⊥l.
(1)求动点Q的轨迹C的方程;
(2)设圆M过A(1,0),且圆心M在曲线C上,TS是圆M在y轴上截得的弦,当M运动时,弦长|TS|是否为定值?请说明理由.

(1)依题意知,点R是线段FP的中点,且RQ⊥FP,
∴RQ是线段FP的垂直平分线.
∵|PQ|是点Q到直线l的距离.
点Q在线段FP的垂直平分线上,
∴|PQ|=|QF|.
故动点Q的轨迹是以F为焦点,l为准线的抛物线,
其方程为y2=2x(x>0).
(2)弦长|TS|为定值.理由如下:取曲线C上点M(x0,y0),
M到y轴的距离为d=|x0|=x0,
 因为点M在曲线C上,
因为点M在曲线C上,
所以x0= ,
,
所以|TS|= =2,是定值.
=2,是定值.

练习册系列答案
相关题目
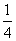 =0
=0
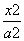 -
-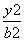 =1(a,b>0)的右焦点F,若过F且倾斜角为60°的直线l与双曲线的右支有且只有1个交点,则此双曲线的离心率e的取值范围是________.
=1(a,b>0)的右焦点F,若过F且倾斜角为60°的直线l与双曲线的右支有且只有1个交点,则此双曲线的离心率e的取值范围是________.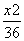 +
+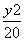 =1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.
=1长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF. -
-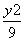 =1上,则
=1上,则 为( )
为( ) B.
B.
 D.
D.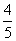
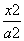 -
-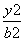 =1(a>0,b>0)相交于A、B、C、D四点,若四边形ABCD为正方形,则双曲线的离心率的取值范围为( )
=1(a>0,b>0)相交于A、B、C、D四点,若四边形ABCD为正方形,则双曲线的离心率的取值范围为( )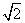 ) B.(1,
) B.(1,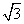 )
)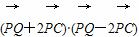 =0.
=0.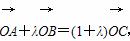 ,求λ的取值范围.
,求λ的取值范围.