题目内容
空间四边形ABCD的两条对角线AC，BD的长分别为4，5，则平行于两条对角线的截面四边形EFGH在平移过程中，其周长的取值范围是（ ）
| A、（5，10） |
| B、（8，10） |
| C、（3，6） |
| D、（6，9） |
考点：平行投影及平行投影作图法
专题：计算题,空间位置关系与距离
分析：设出参变量（比例），利用有关比例性质建立函数关系，根据k的范围0＜k＜1（当点H与重合时k=0但取不到0，当H与A重合时k=1，但取不到1），从而可得结果．
解答：
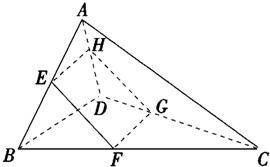解：如图所示，设
=
=k，∴
=
=1-k，
∴GH=4k，EH=5（1-k），∴周长=8+2k．
又∵0＜k＜1，∴周长的范围为（8，10）．
故选：B．
解：如图所示，设| DH |
| DA |
| GH |
| AC |
| AH |
| DA |
| EH |
| BD |
∴GH=4k，EH=5（1-k），∴周长=8+2k．
又∵0＜k＜1，∴周长的范围为（8，10）．
故选：B．
点评：本题主要考查棱锥的结构特征，特别考查了截面问题，三角形相似以及建模和解模的能力，属中档题．
练习册系列答案
相关题目
设a=2
，b=ln2，c=log2
，则a，b，c的大小关系是（ ）
| 5 |
| 2 |
| 1 |
| 3 |
| A、a＞c＞b |
| B、c＞a＞b |
| C、b＞a＞c |
| D、a＞b＞c |
值域是（0，+∞）的函数是（ ）
A、y=（
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
已知函数sgn（x）=
，f（x）=x2•sgn（x）+x•sgn（-x），若函数g（x）=f（x）-m有三个零点，则m的取值范围是（ ）
|
A、m＜-
| ||
B、-
| ||
C、0＜m＜
| ||
D、m＞
|
圆柱的一个底面面积为π，侧面展开图是一个正方形，则这个圆柱的体积为（ ）
| A、π |
| B、2π |
| C、π2 |
| D、2π2 |
曲线y=1+
与直线kx-y+4-2k=0有两个交点，则实数k的取值范围是（ ）
| 4-x2 |
A、（0，
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
圆C：x2+y2-2x-4y+4=0上的点到直线-3x+4y+14=0的距离的最大值是（ ）
| A、4 | B、5 | C、6 | D、8 |