题目内容
已知函数sgn(x)=
,f(x)=x2•sgn(x)+x•sgn(-x),若函数g(x)=f(x)-m有三个零点,则m的取值范围是( )
|
A、m<-
| ||
B、-
| ||
C、0<m<
| ||
D、m>
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:函数g(x)=f(x)-m零点的个数,即函数y=f(x)与y=m的图象交点的个数,画出函数图象,数形结合可得答案.
解答:
 解:∵sgn(x)=
解:∵sgn(x)=
,
∴f(x)=x2•sgn(x)+x•sgn(-x)=
.
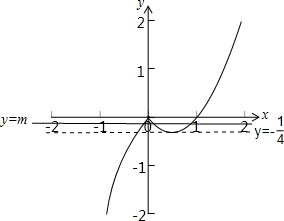
故函数的图象如下图所示:
由图可得:当-
<m<0时,函数y=f(x)与y=m的图象有三个交点,
即函数g(x)=f(x)-m有三个零点,
故选:B
 解:∵sgn(x)=
解:∵sgn(x)=
|
∴f(x)=x2•sgn(x)+x•sgn(-x)=
|
故函数的图象如下图所示:
由图可得:当-
| 1 |
| 4 |
即函数g(x)=f(x)-m有三个零点,
故选:B
点评:本题考查的知识点是根的存在性及根的个数判断,其中熟练掌握函数零点与方程根之间的对应关系是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等比数列{an}满足a1=4,公比q=-
,则{an}的前10项和等于( )
| 1 |
| 3 |
| A、-6(1-3-10) | ||
B、
| ||
| C、3(1-3-10) | ||
| D、3(1+3-10) |
已知双曲线
-
=1(a>0,b>0)的两个焦点分别为F1、F2,以线段F1F2为直径的圆与双曲线渐近线的一个交点为(4,3),则此双曲线的方程为( )
| y2 |
| a2 |
| x2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设x,y满足不等式组
,若Z=ax+y的最大值为2a+9,最小值为a+2,则实数a的取值范围是( )
|
| A、(-∞,-7] |
| B、[-3,1] |
| C、[1,+∞) |
| D、[-7,-3] |
(文科)若等腰直角三角形的直角边长为2,则以斜边所在的直线为轴旋转一周所成的几何体体积是( )
A、4
| ||||
B、
| ||||
C、
| ||||
| D、4π |
复数z=i(1-2i)(i为虚数单位),则z的共轭复数
为( )
. |
| z |
| A、2-i | B、2+i |
| C、4-2i | D、4+2i |
空间四边形ABCD的两条对角线AC,BD的长分别为4,5,则平行于两条对角线的截面四边形EFGH在平移过程中,其周长的取值范围是( )
| A、(5,10) |
| B、(8,10) |
| C、(3,6) |
| D、(6,9) |
已知函数f(x)的图象是连续不断的一条曲线,若f(-1)•f(3)<0,则( )
| A、方程f(x)=0一定有两实根 |
| B、方程f(x)=0一定无实数根 |
| C、方程f(x)=0一定有实数根 |
| D、方程f(x)=0可能无实数根 |