题目内容
16．sin1290°=（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | -$\frac{1}{2}$ |
分析 根据诱导公式，转化成锐角的三角函数形式再计算即可．
解答 解：sin1290°=sin（360°×3+210°）=sin210°=sin（180°+30°）=-sin30°=-$\frac{1}{2}$．
故选：D．
点评 本题考查诱导公式的化简求值．对角的转化原则是：负（角）化正（角），大（角）化小（角），属于基础题．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
8．要得到函数y=2cosx•sin（x+$\frac{π}{6}$）-$\frac{1}{2}$的图象，只需将y=sinx的图象（ ）
| A． | 先向左平移$\frac{π}{6}$个单位长度，再将所有点的横坐标缩短为原来的$\frac{1}{2}$倍（纵坐标不变） | |
| B． | 先向左平移$\frac{π}{6}$个单位长度，再将所有点的横坐标缩短为原来的2倍（纵坐标不变） | |
| C． | 先将所有点的横坐标缩短为原来的2倍（纵坐标不变），再向左平移$\frac{π}{6}$个单位长度 | |
| D． | 先将所有点的横坐标缩短为原来的$\frac{1}{2}$倍（纵坐标不变），再向左平移$\frac{π}{6}$个单位长度 |
5．函数f（x）=3sin（ωx+φ）的部分图象如图，则f（x）的单调递增区间为（ ）
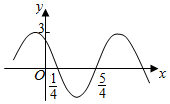
| A． | （kπ-$\frac{5}{4}$，kπ-$\frac{1}{4}$），k∈Z | B． | （2kπ-$\frac{5}{4}$，2kπ-$\frac{1}{4}$），k∈Z | ||
| C． | （2k-$\frac{5}{4}$，2k-$\frac{1}{4}$），k∈Z | D． | （k-$\frac{5}{4}$，k-$\frac{1}{4}$），k∈Z |