题目内容
10.解方程:log3(x+14)+log3(x+2)=log38(x+6)分析 利用对数的运算法则得到log3[(x+14)(x+2)]=log38(x+6),由此利用对数的性质列出不等式组,能求出方程的解.
解答 解:∵log3(x+14)+log3(x+2)=log38(x+6),
∴log3[(x+14)(x+2)]=log38(x+6),
∴$\left\{\begin{array}{l}{x+14>0}\\{x+2>0}\\{x+6>0}\\{(x+14)(x+2)=8(x+6)}\end{array}\right.$,
解得x=2.
点评 本题考查对数方程的解法,是基础题,解题时要认真审题,注意对数的性质、运算法则的合理运用.

练习册系列答案
相关题目
20.已知A,B,C是复平面内的三个不同点,点A,B对应的复数分别是-2+3i,-i,若$\overrightarrow{AC}$=$\overrightarrow{CB}$,则点C表示的复数是( )
| A. | -2+2i | B. | -2+4i | C. | -1+i | D. | -1+2i |
5.函数f(x)=3sin(ωx+φ)的部分图象如图,则f(x)的单调递增区间为( )
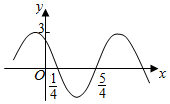

| A. | (kπ-$\frac{5}{4}$,kπ-$\frac{1}{4}$),k∈Z | B. | (2kπ-$\frac{5}{4}$,2kπ-$\frac{1}{4}$),k∈Z | ||
| C. | (2k-$\frac{5}{4}$,2k-$\frac{1}{4}$),k∈Z | D. | (k-$\frac{5}{4}$,k-$\frac{1}{4}$),k∈Z |
3.在区间(0,100)上任取一数x,则lg x>1的概率是( )
| A. | 0.1 | B. | 0.5 | C. | 0.8 | D. | 0.9 |
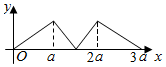
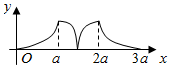
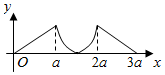
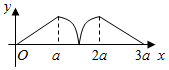
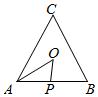 如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )
如图所示,点P从点A处出发,按逆时针方向沿边长为a的正三角形ABC运动一周,O为ABC的中心,设点P走过的路程为x,△OAP的面积为f(x)(当A、O、P三点共线时,记面积为0),则函数f(x)的图象大致为( )