题目内容
3.己知实数x,y满足约束条件$\left\{\begin{array}{l}{5x+3y≤15}\\{y≤x+1}\\{x-5y≤3}\end{array}\right.$,若目标函数z=3x+ay在点A($\frac{3}{2}$,$\frac{5}{2}$)取得最大值,则a的取值范围是($\frac{9}{5},+∞$).分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,结合题意列关于a的不等式组,求解不等式组得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{5x+3y≤15}\\{y≤x+1}\\{x-5y≤3}\end{array}\right.$作出可行域如图,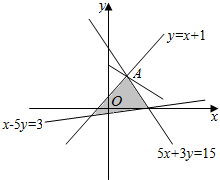
由z=3x+ay,得y=$-\frac{3}{a}x+\frac{z}{a}$,
要使目标函数z=3x+ay在点A($\frac{3}{2}$,$\frac{5}{2}$)取得最大值,
则$\left\{\begin{array}{l}{a>0}\\{-\frac{3}{a}>-\frac{5}{3}}\end{array}\right.$,解得a$>\frac{9}{5}$.
故答案为:($\frac{9}{5},+∞$).
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
14.“$\frac{|C|}{\sqrt{A^2+B^2}}$≤a”是“曲线Ax+By+C=0与$\frac{x^2}{a}$+$\frac{y^2}{b}$=1(a>b>0)有公共点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.设偶函数f(x)在[0,+∞)上为增函数,则不等式f(x)>f(2x十1)的解集为( )
| A. | ∅ | B. | {x|x<-1或x>$\frac{1}{3}$} | C. | {x|x>1或x<$\frac{1}{3}$} | D. | {x|-1<x<-$\frac{1}{3}$} |
18.${∫}_{0}^{π}$(sin2x-cosx)dx的值为( )
| A. | 1 | B. | 0 | C. | 2 | D. | -2 |
15.已知数列{an}中,a3=2,a7=1,又数列{$\frac{1}{{a}_{n}}$}是等差数列,则a12等于( )
| A. | $\frac{13}{8}$ | B. | $\frac{8}{13}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
12.若α,β为不重合的两个平面,m,n为不重合的两条直线,则下列命题中正确的是( )
| A. | 苦m∥n,n?α,则m∥α | B. | 若m∥n,m?α,n⊥β,则α⊥β | ||
| C. | 若α∥β,m?α,n?β,则m∥n | D. | 若α⊥β,m?α,则m⊥β |