题目内容
1.若三棱锥S-ABC的所有的顶点都在球O的球面上.SA⊥平面ABC.SA=AB=2,AC=4,∠BAC=$\frac{π}{3}$,则球O的表面积为20π.分析 由余弦定理求出BC=2$\sqrt{3}$,利用正弦定理得∠ABC=90°.从而△ABC截球O所得的圆O′的半径r=$\frac{1}{2}$AC=2,进而能求出球O的半径R,由此能求出球O的表面积.
解答 解:如图,三棱锥S-ABC的所有顶点都在球O的球面上,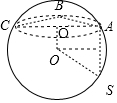
∵SA⊥平面ABC.SA=AB=2,AC=4,∠BAC=$\frac{π}{3}$,
∴BC=$\sqrt{4+16-2×2×4×cos\frac{π}{3}}$=2$\sqrt{3}$,
∴AC2=BC2+AB2,∴∠ABC=90°.
∴△ABC截球O所得的圆O′的半径r=$\frac{1}{2}$AC=2,
∴球O的半径R=$\sqrt{{2}^{2}+(\frac{2}{2})^{2}}$=$\sqrt{5}$,
∴球O的表面积S=4πR2=20π.
故答案为:20π.
点评 本题考查三棱锥、球、勾股定理等基础知识,考查抽象概括能力、数据处理能力、运算求解能力,考查应用意识、创新意识,考查化归与转化思想、分类与整合思想、数形结合思想,是中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
9.已知正方体ABCD-A1B1C1D1的各顶点都在球O表面上,在球O内任取一点M,则点M在正方体ABCD-A1B1C1D1内的概率是( )
| A. | $\frac{3\sqrt{2}}{4π}$ | B. | $\frac{3\sqrt{2}}{2π}$ | C. | $\frac{\sqrt{3}}{3π}$ | D. | $\frac{2\sqrt{3}}{3π}$ |
6.设向量前$\overrightarrow{BA}$=(3,-2),$\overrightarrow{AC}$=(0,6),则|$\overrightarrow{BC}$|等于( )
| A. | 2$\sqrt{6}$ | B. | 5 | C. | $\sqrt{26}$ | D. | 6 |
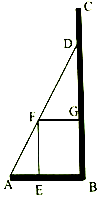 如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.
如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1,种花的面积为S2,比值$\frac{{S}_{1}}{{S}_{2}}$称为“规划和谐度”.